题目内容
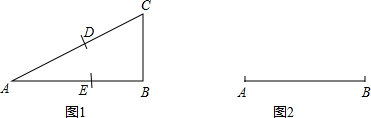
(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证:
=
.(这个比值
叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
| AE |
| AB |
| ||
| 2 |
| ||
| 2 |
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)

考点:作图—应用与设计作图,黄金分割
专题:作图题
分析:(1)利用位置数表示出AB,AC,BC的长,进而得出AE的长,进而得出答案;
(2)根据底与腰之比均为黄金比的等腰三角形,画图即可.
(2)根据底与腰之比均为黄金比的等腰三角形,画图即可.
解答:(1)证明:∵Rt△ABC中,∠B=90°,AB=2BC,
∴设AB=2x,BC=x,则AC=
x,
∴AD=AE=(
-1)x,
∴
=
=
.
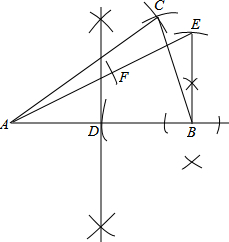
(2)解:底与腰之比均为黄金比的等腰三角形,如图:
①过点B作EB⊥AB,作AB的垂直平分线交AB于点D,使BE=BD,
②连接AE,以E为圆心,BE长为半径画弧,使EF=BE,
③以B为圆心AF长为半径画弧,以A为圆心,AB长为半径画弧,交点为C,
则△ABC即为所求.
 .
.
∴设AB=2x,BC=x,则AC=
| 5 |
∴AD=AE=(
| 5 |
∴
| AE |
| AB |
(
| ||
| 2x |
| ||
| 2 |
(2)解:底与腰之比均为黄金比的等腰三角形,如图:
①过点B作EB⊥AB,作AB的垂直平分线交AB于点D,使BE=BD,
②连接AE,以E为圆心,BE长为半径画弧,使EF=BE,
③以B为圆心AF长为半径画弧,以A为圆心,AB长为半径画弧,交点为C,
则△ABC即为所求.
 .
.点评:此题主要考查了黄金三角形的作法以及黄金三角形的性质,根据已知得出底边作法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
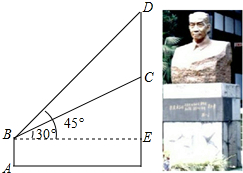 如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: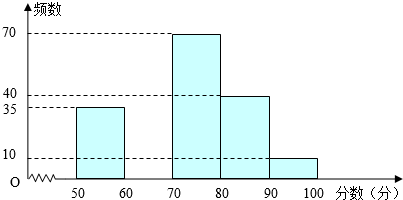
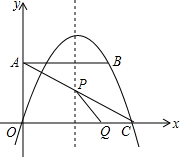 如图,平面直角坐标系中,四边形OABC是直角梯形,AB∥OC,OA=5,AB=10,OC=12,抛物线y=ax2+bx经过点B、C.
如图,平面直角坐标系中,四边形OABC是直角梯形,AB∥OC,OA=5,AB=10,OC=12,抛物线y=ax2+bx经过点B、C.