题目内容
(1)计算:
×
-4×
×(1-
)0;
(2)先化简,再求值:(
+
)÷
,其中a,b满足
+|b-
|=0.
| 24 |
|
|
| 2 |
(2)先化简,再求值:(
| a2-b2 |
| a2-2ab+b2 |
| a |
| b-a |
| b2 |
| a2-ab |
| a+1 |
| 3 |
考点:二次根式的混合运算,非负数的性质:绝对值,非负数的性质:算术平方根,分式的化简求值,零指数幂
专题:计算题
分析:(1)根据二次根式的乘法法则和零指数幂的意义得到原式=
-4×
×1=2
-
,然后合并即可;
(2)先把分子和分母因式分解和除法运算化为乘法运算,再计算括号内的运算,然后约分得到原式=
,再根据非负数的性质得到a+1=0,b-
=0,解得a=-1,b=
,然后把a和b的值代入计算即可.
24×
|
| ||
| 4 |
| 2 |
| 2 |
(2)先把分子和分母因式分解和除法运算化为乘法运算,再计算括号内的运算,然后约分得到原式=
| a |
| b |
| 3 |
| 3 |
解答:解:(1)原式=
-4×
×1
=2
-
=
;
(2)原式=[
-
]•
=(
-
)•
=
•
=
,
∵
+|b-
|=0,
∴a+1=0,b-
=0,
解得a=-1,b=
,
当a=-1,b=
时,原式=-
=-
24×
|
| ||
| 4 |
=2
| 2 |
| 2 |
=
| 2 |
(2)原式=[
| (a+b)(a-b) |
| (a-b)2 |
| a |
| a-b |
| a(a-b) |
| b2 |
=(
| a+b |
| a-b |
| a |
| a-b |
| a(a-b) |
| b2 |
=
| b |
| a-b |
| a(a-b) |
| b2 |
=
| a |
| b |
∵
| a+1 |
| 3 |
∴a+1=0,b-
| 3 |
解得a=-1,b=
| 3 |
当a=-1,b=
| 3 |
| 1 | ||
|
| ||
| 3 |
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂、非负数的性质和分式的化简求值.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知:a2-3a+1=0,则a+
-2的值为( )
| 1 |
| a |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、-5 |
 如图,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD=
如图,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD= 如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为
如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为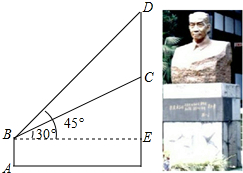 如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: