题目内容
7.若(a+3b-5)2+|3a-2b-4|=0,则a=2,b=1.分析 根据非负数性质可得关于a、b的方程组,解方程组可得a、b的值.
解答 解:由非负数性质可得:$\left\{\begin{array}{l}{a+3b-5=0}&{①}\\{3a-2b-4=0}&{②}\end{array}\right.$,
①×3-②,得:11b-11=0,
解得:b=1,
将b=1代入①,得:a+3-5=0,
解得:a=2,
∴a=2,b=1,
故答案为:2,1.
点评 本题主要考查的是非负数的性质,即几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
13.若(x-3)(x+5)=x2+ax+b,则a+b的值是( )
| A. | -13 | B. | 13 | C. | 2 | D. | -15 |
17. 如图是由一水桶抽象而成的几何图形,其俯视图是( )
如图是由一水桶抽象而成的几何图形,其俯视图是( )
 如图是由一水桶抽象而成的几何图形,其俯视图是( )
如图是由一水桶抽象而成的几何图形,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
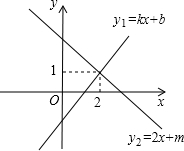 直线y1=kx+b和y2=2x+m相交于点A(2,1).
直线y1=kx+b和y2=2x+m相交于点A(2,1).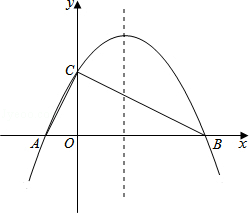 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(-2,0).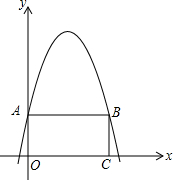 如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.
如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.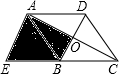 如图,在菱形ABCD中,对角线AC和BD的长分别为8和6,将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,则阴影部分的面积为18.
如图,在菱形ABCD中,对角线AC和BD的长分别为8和6,将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,则阴影部分的面积为18.