题目内容
16.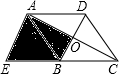 如图,在菱形ABCD中,对角线AC和BD的长分别为8和6,将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,则阴影部分的面积为18.
如图,在菱形ABCD中,对角线AC和BD的长分别为8和6,将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,则阴影部分的面积为18.
分析 直接利用菱形的性质得出其面积,进而得出S△ABO,再利用平移的性质得出S△AEB=$\frac{1}{2}$S四边形AEBD=$\frac{1}{2}$S菱形ABCD,进而得出答案.
解答 解:∵在菱形ABCD中,对角线AC和BD的长分别为8和6,
∴菱形ABCD的面积为:$\frac{1}{2}$×6×8=24,
∴S△ABO=$\frac{1}{4}$×24=6,
∵将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,
∴四边形AEBD是菱形,
∴S△AEB=$\frac{1}{2}$S四边形AEBD=$\frac{1}{2}$S菱形ABCD=12,
∴阴影部分的面积为:18.
故答案为:18.
点评 此题主要考查了平移的性质以及菱形的性质,正确应用菱形的面积公式是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
5.若$\sqrt{{-(1-a)}^{2}}$有意义,则满足条件的a的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
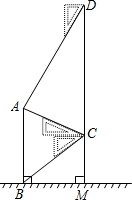 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).