题目内容
18.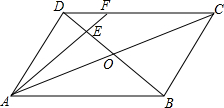 如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )| A. | 1:3 | B. | 1:5 | C. | 1:6 | D. | 1:11 |
分析 根据平行四边形的性质可知BO=DO,又因为E为OD的中点,所以DE:BE=1:3,根据相似三角形的性质可求出S△DEF:S△BAE.然后根据$\frac{{S}_{△AOB}}{{S}_{△ABE}}$=$\frac{2}{3}$,即可得到结论.
解答 解:∵O为平行四边形ABCD对角线的交点,
∴DO=BO,
又∵E为OD的中点,
∴DE=$\frac{1}{4}$DB,
∴DE:EB=1:3,
又∵AB∥DC,
∴△DFE∽△BAE,
∴$\frac{{S}_{△DEF}}{{S}_{△BAE}}$=($\frac{1}{3}$)2=$\frac{1}{9}$,
∴S△DEF=$\frac{1}{9}$S△BAE,
∵$\frac{{S}_{△AOB}}{{S}_{△ABE}}$=$\frac{2}{3}$,
∴S△AOB=$\frac{2}{3}$S△BAE,
∴S△DEF:S△AOB=$\frac{\frac{1}{9}{S}_{△BAE}}{\frac{2}{3}{S}_{△BAE}}$=1:6,
故选C.
点评 题考查了相似三角形的判定与性质以及平行四边形的性质,难度适中,解答本题的关键是根据平行证明△DFE∽△BAE,然后根据对应边成比例求值.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
6.(-3)×2的结果是( )
| A. | -5 | B. | -6 | C. | -1 | D. | 6 |
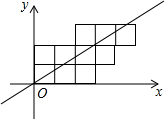 如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为y=$\frac{9}{14}$x.
如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为y=$\frac{9}{14}$x.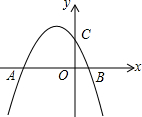 已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c与y轴交于点C,与x轴的两个交点分别为A(-4,0),B(1,0).
已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c与y轴交于点C,与x轴的两个交点分别为A(-4,0),B(1,0).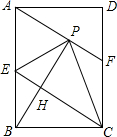 如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H.
如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H. 如图,一束平行太阳光照射到等边三角形上,若∠α=28°,则∠β=32°.
如图,一束平行太阳光照射到等边三角形上,若∠α=28°,则∠β=32°. 如图,矩形ABCD中,点O在BC上,OB=2OC=2,以O为圆心OB的长半径画弧,这条弧恰好经过点D,则图中阴影部分的面积为$\frac{2π}{3}$-$\sqrt{3}$.
如图,矩形ABCD中,点O在BC上,OB=2OC=2,以O为圆心OB的长半径画弧,这条弧恰好经过点D,则图中阴影部分的面积为$\frac{2π}{3}$-$\sqrt{3}$.