题目内容
8. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
分析 由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′,∠AOA′=90°,作AC⊥y轴于C,A′C′⊥x轴于C′,就可以得出△ACO≌△A′C′O,就可以得出AC=A′C′,CO=C′O,由A的坐标就可以求出结论.
解答 解:∵线段AB绕点O顺时针旋转90°得到线段A′B′,
∴△ABO≌△A′B′O′,∠AOA′=90°,
∴AO=A′O.
作AC⊥y轴于C,A′C′⊥x轴于C′,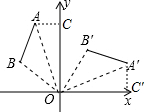 ∴∠ACO=∠A′C′O=90°.
∴∠ACO=∠A′C′O=90°.
∵∠COC′=90°,
∴∠AOA′-∠COA′=∠COC′-∠COA′,
∴∠AOC=∠A′OC′.
在△ACO和△A′C′O中,
$\left\{\begin{array}{l}{∠ACO=∠A′C′O}\\{∠AOC=∠A′OC′}\\{AO=A′O}\end{array}\right.$,
∴△ACO≌△A′C′O(AAS),
∴AC=A′C′,CO=C′O.
∵A(-2,5),
∴AC=2,CO=5,
∴A′C′=2,OC′=5,
∴A′(5,2).
故选:B.
点评 本题考查了旋转的性质的运用,全等三角形的判定及性质的运用,等式的性质的运用,点的坐标的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
18.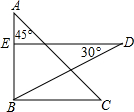 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )| A. | 内部 | B. | 外部 | C. | 边上 | D. | 以上都有可能 |
19.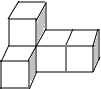 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )| A. | 主视图的面积最小 | B. | 左视图的面积最小 | ||
| C. | 俯视图的面积最小 | D. | 三个视图的面积相等 |
20.我市气象部门测得某周内七天的日温差数据如下:4,6,6,5,7,6,8(单位:℃),这组数据的平均数和众数分别是( )
| A. | 7,6 | B. | 6,5 | C. | 5,6 | D. | 6,6 |
17.下列备选答案的四个数中,最大的一个是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
18.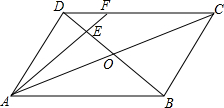 如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
 如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )| A. | 1:3 | B. | 1:5 | C. | 1:6 | D. | 1:11 |
 如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )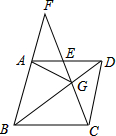 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.