题目内容
10.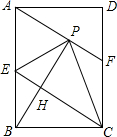 如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H.
如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连结AP并延长AP交CD于F点,连接BP,交CE于点H.(1)若∠PBA:∠PBC=1:2,判断△PBC的形状并说明;
(2)求证:四边形AECF为平行四边形.
分析 (1)根据矩形得出∠ABC=90°,求出∠OBC=60°,根据折叠得出PC=BC,根据等边三角形的判定得出即可;
(2)根据折叠得出BE=PE,求出∠1=∠2,求出AE=PE,推出∠3=∠4,根据三角形内角和定理求出∠2+∠3=90°,求出AF∥CE,根据平行四边形的判定得出即可.
解答 (1)解:△PBC是等边三角形,
理由是:在矩形ABCD中,∠ABC=90°,
∵∠PBA:∠PBC=1:2,
∴∠OBC=60°,
∵沿EC对折矩形ABCD,使B点落在点P处,
∴PC=BC,
∴△PBC是等边三角形;
(2)证明:
∵根据折叠得出△EBC≌△EPC,
∴BE=PE,
∴∠1=∠2,
∵E为AB的中点,
∴BE=AE,
∴AE=PE,
∴∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∴BP⊥AF,
∵对折矩形ABCD,
∴BP⊥CE,
∴AF∥CE,
∵根据矩形ABCD得:AE∥CF,
∴四边形AECF为平行四边形.
点评 本题考查了矩形的性质,折叠的性质,等边三角形的判定,平行四边形的判定的应用,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
20.我市气象部门测得某周内七天的日温差数据如下:4,6,6,5,7,6,8(单位:℃),这组数据的平均数和众数分别是( )
| A. | 7,6 | B. | 6,5 | C. | 5,6 | D. | 6,6 |
1.已知α为锐角,sinα=$\frac{1}{2}$,则α等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
18.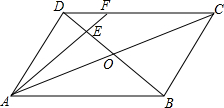 如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
 如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
如图,在?ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )| A. | 1:3 | B. | 1:5 | C. | 1:6 | D. | 1:11 |
2.下列运算中,结果正确的是( )
| A. | 2a+3b=5ab | B. | a2•a3=a6 | C. | (a4)2=a8 | D. | a6÷a3=a2 |
19.若|x|=2016,则x等于( )
| A. | -2016 | B. | 2016 | C. | $\frac{1}{2016}$ | D. | ±2016 |
20. 如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )
如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )
 如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )
如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )| A. | 15° | B. | 20 | C. | 30° | D. | 40 |
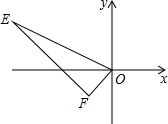 如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).
如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).