题目内容
14．
如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=40°，则∠AEF=110°．
分析 根据折叠的性质及∠1=40°可求出∠2的度数，再由平行线的性质即可解答．
解答 
解：∵四边形EFGH是四边形EFBA折叠而成，
∴∠2=∠3，
∵∠2+∠3+∠1=180°，∠1=40°，
∴∠2=∠3=$\frac{1}{2}$（180°-40°）=$\frac{1}{2}$×140°=70°，
又∵AD∥BC，
∴∠AEF+∠EFB=180°，
∴∠AEF=180°-70°=110°．
故答案为：110°
点评 本题主要考查了平行线的性质和折叠的性质，解题时注意：折叠前后的图形全等，找出图中相等的角是解答此题的关键．
练习册系列答案
相关题目
3．函数y=$\sqrt{3-x}$+$\frac{1}{x-2}$中自变量x的取值范围是（ ）
| A． | x≤3 | B． | x＜3且x≠2 | C． | x≤3且x≠2 | D． | x≠2 |
4．下列运算正确的是（ ）
| A． | x2•x6=x12 | B． | （-6x6）÷（-2x2）=3x3 | C． | 2a-3a=-a | D． | （x-2）2=x2-4 |
2．
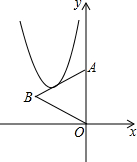如图，抛物线y=2x2+bx+c的顶点在△OAB的边OB、AB上运动（不经过点O，点A），已知A（0，2），B（-2，1），则下列说法错误的是（ ）
如图，抛物线y=2x2+bx+c的顶点在△OAB的边OB、AB上运动（不经过点O，点A），已知A（0，2），B（-2，1），则下列说法错误的是（ ）| A． | 0＜b≤8 | B． | 0＜c≤9 | C． | 1+2c＞b | D． | b2＜8c-16 |
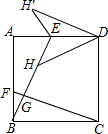如图，正方形ABCD的边长为3，点E、F分别在边AD、AB上且AE=BF=1，连接BE、CF交于点G，在线段EG上取一点H使HG=BG，连接DH，把△EDH沿AD边翻折得到△EDH’，则点H到边DH’的距离是$\frac{24}{25}\sqrt{5}$．
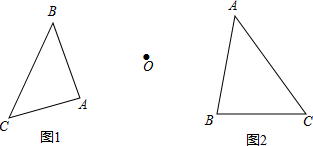如图，已知△ABC，（1）图1中以点O为旋转中心顺时针旋转60°的图形．