题目内容
6.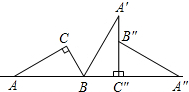 如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2$\sqrt{3}$,则顶点A运动到点A″的位置时,点A经过的路线长是$\frac{8π}{3}$+$\sqrt{3}$π.
如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2$\sqrt{3}$,则顶点A运动到点A″的位置时,点A经过的路线长是$\frac{8π}{3}$+$\sqrt{3}$π.
分析 首先在直角三角形ABC中利用勾股定理求得AB的长,利用三角函数求得∠ABC的度数,然后利用弧长公式即可求解.
解答 解:在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,
又∵BC=2,即$\frac{BC}{AB}=\frac{1}{2}$
∴∠BAC=30°,∠ABC=60°,
由分析知:点A经过的路程是由两段弧长所构成的:
①A~A′段的弧长:L1=$\frac{120π×4}{180}$=$\frac{8π}{3}$,
②A′~A″段的弧长:L2=$\frac{90π×2\sqrt{3}}{180}$=$\sqrt{3}$π,
∴点A所经过的路线为$\frac{8π}{3}$+$\sqrt{3}$π.
故答案是:$\frac{8π}{3}$+$\sqrt{3}$π.
点评 本题考查了弧长的计算以及勾股定理,正确理解弧长的计算公式是本题的关键.

练习册系列答案
相关题目
14.下列语句:
①如果两个图形全等,那么这两个图形一定关于某直线对称;
②等腰三角形的两底角相等;
③有一个角为60°的等腰三角形是等边三角形;
④在等腰△ABC中,若∠B=70°,则∠C=70°.
其中正确的有( )
①如果两个图形全等,那么这两个图形一定关于某直线对称;
②等腰三角形的两底角相等;
③有一个角为60°的等腰三角形是等边三角形;
④在等腰△ABC中,若∠B=70°,则∠C=70°.
其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16.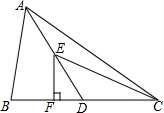 在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
 在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )| A. | 1.2 | B. | 2.4 | C. | 3.6 | D. | 4.8 |




 如图所示,按要求画图.
如图所示,按要求画图.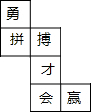 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图,是一个正方体的平面展开图,若图中的“才”表示正方体的前面,“拼”表示正方体的左面,“会”表示上面,则“勇”“搏”分别表示正方体的后面、下面.
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图,是一个正方体的平面展开图,若图中的“才”表示正方体的前面,“拼”表示正方体的左面,“会”表示上面,则“勇”“搏”分别表示正方体的后面、下面.