题目内容
13．商场某种新商品每件进价是120元，在试销售期间发现，当每件商品售价为130元时，每天可销售70件，当每件商品售价高于130元时，每涨价1元，日销售量就减少1件．据此规律，请回答：（1）当每件商品售价定为170元时，每天可销售30件商品，商场获得的日盈利是1500元．
（2）在上述条件不变，商品销售正常的情况下，请问：当每件商品的销售价定为多少元时，能使商场的日盈利最多？（提示：盈利=售价-进价）
分析 （1）先求出提高的价格170-130=40元，就可以求出此时销售减少的数量，就可以求出销售的数量，在由每件利润×件数就可以得出日利润；
（2）设每件商品的售价为x元，则每天销售商品的件数为70-（x-130）=200-x件，根据“总利润=单件利润×销售量”得出函数关系式，再配方即可得其最值情况．
解答 解：（1）由题意得：每天销售的数量为70-（170-130）=30件，
日盈利为：30（170-120）=1500元，
故答案为：30，1500．
（2）设每件商品的售价为x元，则每天销售商品的件数为70-（x-130）=200-x件，
则商场的日盈利w=（x-120）（200-x）
=-x2+320x-24000
=-（x-160）2+1600，
∴当x=160时，w取得最大值，最大值为1600，
答：当每件商品的销售价定为160元时，能使商场的日盈利最多．
点评 本题考查了列一元二次方程解实际问题的运用，解答时灵活运用销售问题的数量关系是解答的关键．
练习册系列答案
相关题目
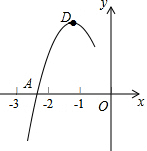抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图所示，则下列结论：①b2-4ac＜0；②a+b+c＜0；③2a+b=0；④c-a=2；⑤4ac-8a=b2；⑥方程ax2+bx+c-1=0有两个相等的实数根．其中正确结论的个数为（ ）