题目内容
1.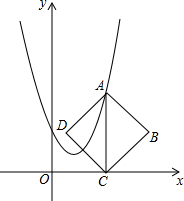 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )| A. | (2,2),(3,5) | B. | (2,2),(4,10) | C. | (3,5),(4,10) | D. | (2,2),(4,10),(6,26) |
分析 设A的坐标为(a,m),由正方形性质可知D(a-$\frac{m}{2}$,$\frac{m}{2}$),根据二次函数图象上点的坐标特征,把A、D的坐标代入解析式得出关于a,m的方程组,解方程组求得a、m的值即可.
解答 解:如图,设A的坐标为(a,m),
∵正方形的对角线相等且互相垂直平分,
∴D(a-$\frac{m}{2}$,$\frac{m}{2}$),
把A、D代入y=x2-2x+2得$\left\{\begin{array}{l}{{a}^{2}-2a+2=m①}\\{(a-\frac{m}{2})^{2}-2(a-\frac{m}{2})+2=\frac{m}{2}②}\end{array}\right.$
由②化简得$\frac{1}{4}$m2+($\frac{1}{2}$-a)m+a2-2a+2=0③,
把①代入③得,$\frac{1}{4}$m2+($\frac{1}{2}$-a)m+m=0,整理得m($\frac{1}{4}$m+$\frac{3}{2}$-a)=0,
∵m≠0,
∴$\frac{1}{4}$m+$\frac{3}{2}$-a=0④,
把①代入④整理得a2-6a+8=0,
解得a=2或4,
∴A(2,2)或(4,10),
故选B.
点评 本题考查了正方形的性质,二次函数图象上点的坐标特征,根据正方形的性质得出D的坐标是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
11.从一幅扑克牌中随机抽取一张牌,它是黑桃的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{27}$ | D. | $\frac{13}{54}$ |
12.半径为30cm,圆心角为120°的扇形恰好围成圆锥的侧面,则这个圆锥的高是( )
| A. | 20$\sqrt{2}$cm | B. | 20$\sqrt{3}$cm | C. | 60$\sqrt{2}$cm | D. | 60$\sqrt{3}$cm |
6. 如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
 如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )| A. | ∠FEG | B. | ∠EAF | C. | ∠AEF | D. | ∠EFA |
13.在1,0,π,-3这四个数中,最大的数是( )
| A. | 1 | B. | 0 | C. | π | D. | -3 |
10.|-2016|的倒数是( )
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
11.据统计2016年1月至2016年6月,石榴园、台儿庄古城等景区共接待游客约518000人,这个数可用科学记数法表示为( )
| A. | 0.518×104 | B. | 5.18×105 | C. | 51.8×104 | D. | 518×103 |
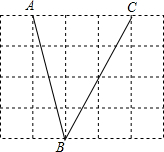 如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请只用一把无刻度直尺作图:①线段AB上画出点P,使AP=$\frac{\sqrt{17}}{3}$;②作△ABC,使点C落在格点上,并且使△ABC的面积为6(只作一个);③作线段CD=$\frac{12\sqrt{17}}{17}$.
如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请只用一把无刻度直尺作图:①线段AB上画出点P,使AP=$\frac{\sqrt{17}}{3}$;②作△ABC,使点C落在格点上,并且使△ABC的面积为6(只作一个);③作线段CD=$\frac{12\sqrt{17}}{17}$.