题目内容
6. 如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )| A. | ∠FEG | B. | ∠EAF | C. | ∠AEF | D. | ∠EFA |
分析 由折叠的性质可知:∠BEG=∠FEG,BE=EF,又点E是AB的中点,故有AE=BE=EF,∠AFE=∠EAF,又2∠BEG=∠AFE+∠EAF,可得:∠BEG=∠EAF=∠EFA,从而得出答案.
解答 解:由折叠的性质可知:∠BEG=∠FEG,BE=EF,
又点E是AB的中点,
∴AE=BE=EF,∠AFE=∠EAF,
又2∠BEG=∠AFE+∠EAF,
∴∠BEG=∠EAF=∠EFA,
∴∠AEF不一定与∠BEG相等,
故选C.
点评 本题考查了折叠的性质以及平行四边形的性质,折叠前后的两个图形全等,即对应角相等,对应线段相等.也考查了若三角形一边上的中线等于这边的一半,则此三角形为直角三角形.

练习册系列答案
相关题目
16.下列现象中,属于平移现象的是( )
| A. | 钟表的指针运动 | B. | 行驶的汽车的车轮 | ||
| C. | 电风扇的转动 | D. | 电梯的升降 |
17.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=2 | C. | $\sqrt{2}×\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{18}$÷$\sqrt{3}$=6 |
1.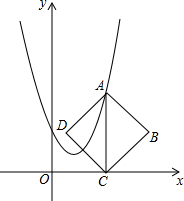 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )| A. | (2,2),(3,5) | B. | (2,2),(4,10) | C. | (3,5),(4,10) | D. | (2,2),(4,10),(6,26) |
11.某商场试销一种新款衬衫,一周内售出型号记录情况如表所示:
商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是( )
| 型号(厘米) | 38 | 39 | 40 | 41 | 42 | 43 |
| 数量(件) | 25 | 30 | 36 | 50 | 28 | 8 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
18.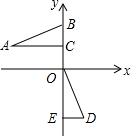 如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |
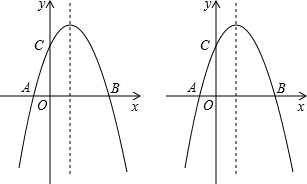 抛物线y=-x2+bx+c经过点A(-1,0)和C(0,3).
抛物线y=-x2+bx+c经过点A(-1,0)和C(0,3).