题目内容
16.设m>n>0,m2+n2=4mn,求$\frac{m+n}{m-n}$的值.分析 根据m2+n2=4mn,求得(m+n)2=6mn,(m-n)2=2mn,又m>n>0,得到m+n=$\sqrt{6mn}$,m-n=$\sqrt{2mn}$,即可解答.
解答 解:∵m2+n2=4mn,
∴(m+n)2=6mn,(m-n)2=2mn,
又∵m>n>0,
∴m+n=$\sqrt{6mn}$,m-n=$\sqrt{2mn}$,
∴$\frac{m+n}{m-n}=\frac{{\sqrt{6mn}}}{{\sqrt{2mn}}}=\sqrt{3}$.
点评 本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.

练习册系列答案
相关题目
4.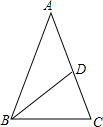 如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
 如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )| A. | 4 | B. | 4$\sqrt{5}$-4 | C. | -4$\sqrt{5}$+4 | D. | 4$\sqrt{5}$-4或-4$\sqrt{5}$+4 |
 如图,△ABC的顶点在网格纸的格点上,则cos∠A=$\frac{2\sqrt{5}}{5}$.
如图,△ABC的顶点在网格纸的格点上,则cos∠A=$\frac{2\sqrt{5}}{5}$.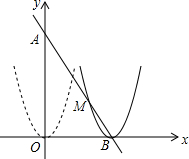 如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B.
如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B. 如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,求证:a∥c.
如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,求证:a∥c.