题目内容
1.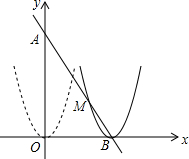 如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B.
如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B.(1)则直线AB的解析式为y1=-2x+12;
平移后的抛物线的解析式为y2=(x-6)2;
(2)求y1<y2时x的取值范围.
分析 (1)首先设直线AB是y=kx+b,利用待定系数法即可求得线段AB所在直线的函数表达式;关键根据平移的性质即可求得平移后的抛物线的解析式;
(2)联立方程,解方程组即可求得交点坐标,根据交点坐标和函数的图象即可求得.
解答 解:(1)设直线AB是y=kx+b,
∵点A、B的坐标是(0,12)、(6,0),
$\left\{\begin{array}{l}{b=12}\\{0=6k+b}\end{array}\right.$,
解得:b=12,k=-2,
∴直线AB的解析式是y=-2x+12;
∵抛物线y=x2沿O→B方向进行平移,平移到B点,向右平移了6个单位,
∴平移后的抛物线的解析式y=(x-6)2;
故答案为:-2x+12,(x-6)2;
(2)解$\left\{\begin{array}{l}{y=-2x+12}\\{y=(x-6)^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=6}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=4}\end{array}\right.$,
∴B(6,0),M(4,4),
∴y1<y2时x的取值范围是x<4或x>6.
点评 本题考查了二次函数图象与几何变换,二次函数的性质,待定系数求一次函数的解析式,熟练掌握平移的性质和待定系数法是解题的关键.

练习册系列答案
相关题目
9.关于一次函数y=ax+$\frac{1}{a}$的下列说法中,正确的个数是( )
①当a<0时,其图象不过第二象限;?
②其图象与x轴正半轴无交点;?
③其图象与线段OA相交,O、A坐标分别为(0,0)、(1,1).
①当a<0时,其图象不过第二象限;?
②其图象与x轴正半轴无交点;?
③其图象与线段OA相交,O、A坐标分别为(0,0)、(1,1).
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.在下列各数中是无理数的有( )
0.333…,$\sqrt{4}$,$\sqrt{5}$,$\frac{1}{3}$,2π,3.14,2.0101010…(相邻两个1之间有1个0)
0.333…,$\sqrt{4}$,$\sqrt{5}$,$\frac{1}{3}$,2π,3.14,2.0101010…(相邻两个1之间有1个0)
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 6个 |
13.对于函数y=x-1,下列结论不正确的是( )
| A. | 图象经过点(-1,-2) | B. | 图象不经过第一象限 | ||
| C. | 图象与y轴交点坐标是(0,-1) | D. | y的值随x值的增大而增大 |
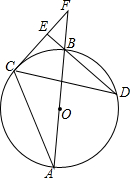 AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.