题目内容
6.已知a2+b2-6a-8b=-25,求a、b的值.分析:“若几个非负数的和为零,则这几个非负数皆为零.”当一个等式里含有几个未知数时,若能将该等式化为几个非负数的和的形式,便能利用上述性质来求解.
例如,将方程a2+b2-6a-8b=-25化为(a-3)2+(b-4)2=0,从而求得a=3,b=4;
再如,将方程a+b-2$\sqrt{a}$-2$\sqrt{b-1}$+1=0化为a-2$\sqrt{a}$+1+(b-1)-2$\sqrt{b-1}$+1=0,再将方程左边配成两个完全平方式的和($\sqrt{a}$-1)2+($\sqrt{b-1}$-1)2=0.从而求得a=1,b=2.
试用类似的方法解决下面的问题:
(1)已知a+b=2$\sqrt{ab}$(a>0,b>0),求$\frac{\sqrt{4a-b}}{\sqrt{5a+7b}}$的值.
(2)已知a+b+c=2$\sqrt{a-2}$+4$\sqrt{b-1}$+6$\sqrt{c+3}$-14,求a、b、c的值.
分析 (1)首先把a+b=2$\sqrt{ab}$,整理得出($\sqrt{a}$-$\sqrt{b}$)2=0,得出a=b,进一步代换求得数值即可;
(2)类比给出的方法将方程左边配成三个完全平方式的和,进一步利用非负数的性质得出a、b、c的值.
解答 解:(1)∵a+b=2$\sqrt{ab}$,
∴($\sqrt{a}$-$\sqrt{b}$)2=0,
∴a=b,
∴$\frac{\sqrt{4a-b}}{\sqrt{5a+7b}}$=$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$.
(2)∵a+b+c=2$\sqrt{a-2}$+4$\sqrt{b-1}$+6$\sqrt{c+3}$-14,
∴a-2-2$\sqrt{a-2}$+1+b-1-4$\sqrt{b-1}$+4+c+3-6$\sqrt{c+3}$+9=0,
∴($\sqrt{a-2}$-1)2+($\sqrt{b-1}$-2)2+($\sqrt{c+3}$-3)2=0,
∴$\sqrt{a-2}$-1=0,$\sqrt{b-1}$-2=0,$\sqrt{c+3}$-3=0,
∴a=3,b=5,c=6.
点评 此题考查配方法的运用,掌握完全平方公式是解决问题的关键.

练习册系列答案
相关题目
16.已知圆柱的底面半径为2cm,高为4cm,则圆柱的侧面积是( )
| A. | 16cm2 | B. | 16πcm2 | C. | 8πcm2 | D. | 4πcm2 |
17. 如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
 如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )| A. | 10 | B. | 12 | C. | 18 | D. | 24 |
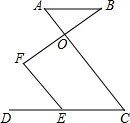 如图,AB∥DC,O是AC上一点,E是CD上一点,F是射线BO上一点,且∠DEF=∠A.
如图,AB∥DC,O是AC上一点,E是CD上一点,F是射线BO上一点,且∠DEF=∠A.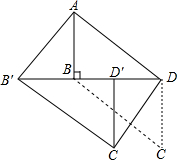 如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.
如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.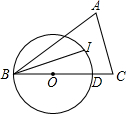 如图,△ABC中,AC=BC,I为△ABC的内心,O为BC上一点,过B、I两点的⊙O交BC于D点,tan∠CBI=$\frac{1}{3}$,AB=6
如图,△ABC中,AC=BC,I为△ABC的内心,O为BC上一点,过B、I两点的⊙O交BC于D点,tan∠CBI=$\frac{1}{3}$,AB=6