题目内容
19.已知一次函数y=mx-m+2,求:(1)m为何值时,它的图象经过原点.
(2)m为何值时,它的图象经过点(0,5).
(3)m为何值时,它的图象不经过第三象限.
分析 (1)一次函数y=kx+b中当b=0时,经过原点;
(2)代入x=0,y=5求得m的值即可;
(3)一次函数y=kx+b中当k<0,b≥0时不经过第三象限;
解答 解:(1)∵一次函数y=mx-m+2的图象经过原点,
∴-m+2=0,
解得:m=2,
∴当m的值为2时,图象经过原点;
(2)当x=0,y=5时,5=-m+2,
解得:m=-3,
所以当m=-3时,y=mx-m+2的图象经过(0,5);
(3)由题意得:$\left\{\begin{array}{l}{m<0}\\{-m+2≥0}\end{array}\right.$,
解得:m<0,
∴当m<0时,图象不经过第三象限.
点评 本题考查了一次函数的图象与系数的关系,解题的关键是了解一次函数的性质,难度不大.

练习册系列答案
相关题目
9.生活中处处有数学,下列原理运用错误的是( )
| A. | 建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理 | |
| B. | 修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理 | |
| C. | 测量跳远的成绩是运用“垂线段最短”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”原理 |
14.为鼓励居民节约用水,某市试行阶梯水价收费制,具体执行方案如下:
例如:一户居民七月份用水12方,则需缴水费12×3.5=42(元).
某户居民六、七月份共用水18方,缴水费54元,已知该用户七月份用水量大于六月份,且六、七月份的用水量均大于5方.问该户居民六、七月份各用水多少方?
| 档次 | 每户每月用水量(方) | 执行水价(元/方) |
| 第一档 | 小于等于5 | 1.5 |
| 第二档 | 大于5小于10 | 2 |
| 第三档 | 大于等于10 | 3.5 |
某户居民六、七月份共用水18方,缴水费54元,已知该用户七月份用水量大于六月份,且六、七月份的用水量均大于5方.问该户居民六、七月份各用水多少方?
11.以一个面积为1的三角形的三条中位线为三边的三角形的面积为( )
| A. | 4 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |

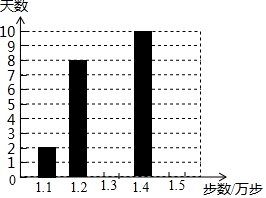 乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).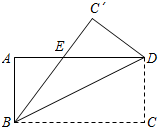 把矩形ABCD沿着对角线BD折叠,使点C落在C′处,交AD于E,若AD=8,AB=4,则AE的长为( )
把矩形ABCD沿着对角线BD折叠,使点C落在C′处,交AD于E,若AD=8,AB=4,则AE的长为( )