题目内容
9.(1)矩形ABCD内有一点P,若PA2+PC2=10,求PB2+PD2的值;(2)由(1)你能得出什么猜想?请说说猜想的依据.
分析 (1)过点P作AD的垂线,交AD于点E,交BC于点F,可证四边形ABFE和CDEF为矩形,则AE=BF,DE=CF,在△PAE,△PCF,△PBF,△PCF中,分别求PA2,PC2,PB2,PD2,再比较PA2+PC2与PB2+PD2即可;
(2)猜想:PA2+PC2=PB2+PD2.
解答 解:(1)过点P作AD的垂线,交AD于点E,交BC于点F,
则四边形ABFE和CDEF为矩形,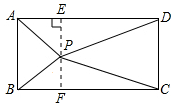
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2=10,
(2)猜想:PA2+PC2=PB2+PD2.
理由:(1)中已经证明.
点评 本题考查了勾股定理及矩形的性质,解题的关键是学会添加辅助线,构造直角三角形,利用勾股定理解决问题,属于中考常考题型.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.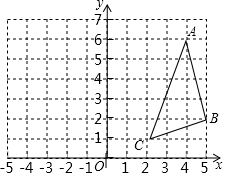 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )| A. | (-3,3)、(-2,4) | B. | (3,-3)、(1,4) | C. | (3,-3)、(-2,4) | D. | (-3,3)、(1,4) |
1.某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )
| A. | 11 | B. | 8 | C. | 7 | D. | 5 |
9.下列各式的变形中,正确的是( )
| A. | x6÷x=x | B. | (x2-$\frac{1}{x}$)÷x=x-1 | C. | x2+x3=x5 | D. | x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$ |
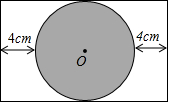 电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.
电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.