��Ŀ����
4��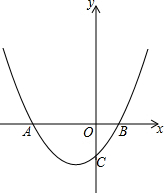 ��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2+6ax-4��x��ĸ������ཻ�ڵ�A����x����������ཻ�ڵ�B����y��ĸ������ཻ�ڵ�C����AB=10��һ�κ���y=x+b���������ཻ�ڵ�E�͵�F����E�ڵ�F��ߣ����������ߵĶԳ����ཻ�ڵ�G��
��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2+6ax-4��x��ĸ������ཻ�ڵ�A����x����������ཻ�ڵ�B����y��ĸ������ཻ�ڵ�C����AB=10��һ�κ���y=x+b���������ཻ�ڵ�E�͵�F����E�ڵ�F��ߣ����������ߵĶԳ����ཻ�ڵ�G����1���������ߵĽ���ʽ��
��2����D��n��n+2����x���·���������һ�㣬����DG��DE����b=8ʱ�����EDG�Ķ�����
��3����bΪ��ֵʱ����������������ֻ��������P��ʹ��EPG�ǵ���ֱ�������Σ�����CF�������ʱ��EFC������ֵ��
���� ��1������AB=10�ɵó�B��A�ĺ�����֮��Ϊ10���������ߵĽ���ʽ������Գ���Ϊ-3��Ҳ�͵ó�A��B�ĺ�����֮��Ϊ-6���Ӷ����A��B�������꣬����ʽҲ����Ȼȷ���ˣ�
��2�������D��G���꣬����A��AH��DG��H������AD�������AH��DH������tan��ADG=$\frac{AH}{DH}$�����ɽ�����⣮
��3����ͼ2�У����E���ڶԳ���ĶԳƵ�ΪP�䣬���ݶԳ��Կ�֪��EGP���ǵ���ֱ�������Σ���E�ǵ���ֱ�������Ρ�EPG��ֱ�Ƕ���ʱ����������������ֻ��������P��ʹ��EPG�ǵ���ֱ�������Σ���ʱ��Pֻ���������߶��㣬�����E��F���꣬��CH��AF��H�����ֱ��CH����ʽ�����÷����������H���꣬���FH��CH���ɽ�����⣮
��� �⣺��1����A��B���������ֱ�Ϊ��x1��0������x2��0����
��AB=10��
��x2-x1=10��
�������߽���ʽΪy=ax2+6ax-4��
�������ߵĶԳ���Ϊx=-$\frac{6a}{2a}$=-3��
��x1+x2=-6��
��x1=-8��x2=2��
����A��-8��0������B��2��0����
����B��2��0�����������߽���ʽ����
0=4a+12a-4����ã�a=$\frac{1}{4}$��
�������ߵĽ���ʽΪy=$\frac{1}{4}$x2+$\frac{3}{2}$x-4��
��2���������⻭��ͼ�Σ���ͼ1��ʾ��
��b=8ʱ��һ�κ�������ʽΪy=x+8��
��y=0������x+8=0����ã�x=-8��
��ʱ��E���A�غϣ�����Ϊ��-8��0����
��x=-3����y=-3+8=5��
��G��������-3��5����
�ߵ�D��n��n+2����x���·���������һ�㣬
��n+2=$\frac{1}{4}{n}^{2}$+$\frac{3}{2}$n-4����n+2��0��
��ã�n=-6����n=4����ȥ����
���D��������-6��-4����
��ֱ��DG�Ľ���ʽΪy=3x+14��
����A��AH��DG��H������AD��
ֱ��AH����ʽΪy=-$\frac{1}{3}$x-$\frac{8}{3}$��
��$\left\{\begin{array}{l}{y=3x+14}\\{y=-\frac{1}{3}x-\frac{8}{3}}\end{array}\right.$���$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$��
���H������-5��-1����
��AH=$\sqrt{��-8+5��^{2}+{1}^{2}}$=$\sqrt{10}$��
DH=$\sqrt{��-6+5��^{2}+��-4+1��^{2}}$=$\sqrt{10}$��
��RT��ADH�У��ߡ�AHD=90�㣬
��tan��ADG=$\frac{AH}{DH}$=1��
���ADG=45�㣮
��3����ͼ2�У����E���ڶԳ���ĶԳƵ�ΪP�䣬���ݶԳ��Կ�֪��EGP���ǵ���ֱ�������Σ�
�൱E�ǵ���ֱ�������Ρ�EPG��ֱ�Ƕ���ʱ����������������ֻ��������P��ʹ��EPG�ǵ���ֱ�������Σ�
��ʱ��Pֻ���������߶��㣬��Ϊ��ʱ��AGP=��APG=45�㣬
���P���꣨-3��-$\frac{25}{4}$����
����P��ֱGE��ֱ�߽���ʽΪy=-x-$\frac{37}{4}$��
��$\left\{\begin{array}{l}{y=-x-\frac{37}{4}}\\{y=\frac{1}{4}{x}^{2}+\frac{3}{2}x-4}\end{array}\right.$���$\left\{\begin{array}{l}{x=-3}\\{y=-\frac{25}{4}}\end{array}\right.$��$\left\{\begin{array}{l}{x=-7}\\{y=-\frac{9}{4}}\end{array}\right.$��
���E����Ϊ��-7��-$\frac{9}{4}$��������y=x+b�õ�b=$\frac{19}{4}$��
����PΪ����ֱ�������Ρ�EPG��ֱ�Ƕ���ʱ����ͼ���֪��P�����ڣ�
��b=$\frac{19}{4}$ʱ����������������ֻ��������P��ʹ��EPG�ǵ���ֱ�������Σ�
��CH��AF��H����ֱ��CH����ʽΪy=-x-4��ֱ��EFΪy=x+$\frac{19}{4}$��
��$\left\{\begin{array}{l}{y=-x-4}\\{y=x+\frac{19}{4}}\end{array}\right.$���$\left\{\begin{array}{l}{x=-\frac{35}{8}}\\{y=\frac{3}{8}}\end{array}\right.$��
���H���꣨-$\frac{35}{8}$��$\frac{3}{8}$����
��HC=$\frac{35}{8}$$\sqrt{2}$��
��$\left\{\begin{array}{l}{y=x+\frac{19}{4}}\\{y=\frac{1}{4}{x}^{2}+\frac{3}{2}x-4}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-7}\\{y=-\frac{9}{4}}\end{array}\right.$��$\left\{\begin{array}{l}{x=5}\\{y=\frac{39}{4}}\end{array}\right.$��
���F���꣨5��$\frac{39}{4}$����
��FH=$\frac{75}{8}$$\sqrt{2}$��
��tan��EFC=$\frac{CH}{FH}$=$\frac{7}{15}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����������Ǻ���������ϵ������֪ʶ������Ĺؼ����������մ���ϵ������ѧ�ṹ�����������÷����������������������꣬ѧ�᳣�ø����ߵ����ӷ����������п�ѹ���⣮

��һ��
| A | B | C | |
| ���� | 85 | 95 | 90 |
| ˵�� | 80 | 85 |
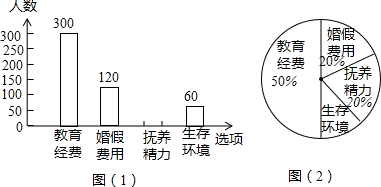
��2��ӦƸ�����һ���������ɸ�У��24����ѧ��ʦ����ͶƱ����λӦƸ�˵ĵ�Ʊ�����ͼ����û����ȨƱ����У��ÿλ��ʦֻ��ѡһλӦƸ��ʦ���������ÿ�˵ĵ�Ʊ������Ʊ����������Ӵ����
��3����ÿƱ��1�֣���У�����ԡ�˵�Ρ���Ʊ������Ե÷ְ�3��4��4�ı���ȷ�����˳ɼ����������λӦƸ�˵����ɼ��������ݳɼ��ж�˭��ӦƸ�ɹ���
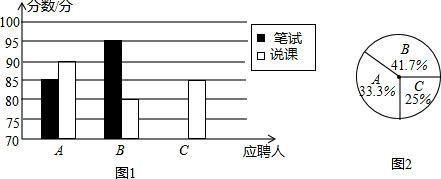
| ѧ�� | A | B | C |
| ���Գɼ�����λ���֣� | 85 | 95 | 90 |
| ���Գɼ�����λ���֣� | 90 | 80 | 85 |

��1���뽫����ͼ1�еĿ�ȱ���ֲ���������
��2����ѡ�����һ���������ɱ��꼶�ε�300��ѧ����������ͶƱ��ÿƱ��1�֣�������ѡ�˵ĵ�Ʊ�����ͼ2��û����ȨƱ��ÿ��ѧ��ֻ���Ƽ�һ�ˣ����������ԡ����ԡ���Ʊ������Ե÷ְ�3��4��3�ı���ȷ�����ɼ��������������ѧ�������ɼ������������ɼ��ж�˭�ܵ�ѡ��
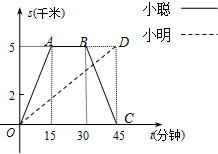 С�ϡ�С�����ֵ�һ��Ӽ��������Ȫ����ͼ��ݲ������ϣ���֪���Ǽҵ���ͼ��ݵ�·����5ǧ�ף�С�������г���С�����У���С�ϴ�ԭ·�ص���ʱ��С���պõ�����ͼ��ݣ�ͼ������O-A-B-C���߶�OD�ֱ��ʾ������ҵ�·��S��ǧ�ף�����������ʱ��t �����ӣ�֮��ĺ�����ϵ�������ͼ��ش��������⣺
С�ϡ�С�����ֵ�һ��Ӽ��������Ȫ����ͼ��ݲ������ϣ���֪���Ǽҵ���ͼ��ݵ�·����5ǧ�ף�С�������г���С�����У���С�ϴ�ԭ·�ص���ʱ��С���պõ�����ͼ��ݣ�ͼ������O-A-B-C���߶�OD�ֱ��ʾ������ҵ�·��S��ǧ�ף�����������ʱ��t �����ӣ�֮��ĺ�����ϵ�������ͼ��ش��������⣺