题目内容
13．先化简：（2x-$\frac{{x}^{2}+1}{x}$）÷$\frac{{x}^{2}-2x+1}{x}$，然后从0，1，-2中选择一个适当的数作为x的值代入求值．分析 先根据分式混合运算的法则把原式进行化简，再选取合适的x的值代入进行计算即可．
解答 解：原式=（$\frac{2{x}^{2}}{x}$-$\frac{{x}^{2}+1}{x}$）÷$\frac{（x-1）^{2}}{x}$
=$\frac{（x+1）（x-1）}{x}$•$\frac{x}{（x-1）^{2}}$
=$\frac{x+1}{x-1}$，
当x=-2时，原式=$\frac{-2+1}{-2-1}$=$\frac{1}{3}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
3．
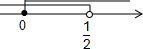一个不等式组中的两个不等式的解集如图所示，则这个不等式组的解集为（ ）
一个不等式组中的两个不等式的解集如图所示，则这个不等式组的解集为（ ）| A． | 0＜x≤$\frac{1}{2}$ | B． | x≤$\frac{1}{2}$ | C． | 0≤x＜$\frac{1}{2}$ | D． | x＞0 |
18．下列计算正确的是（ ）
| A． | 4x-3x=1 | B． | x2+x2=2x4 | C． | （x2）3=x6 | D． | 2x2•x3=2x6 |
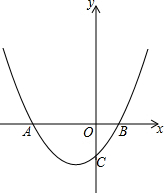如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+6ax-4与x轴的负半轴相交于点A，与x轴的正半轴相交于点B，与y轴的负半轴相交于点C，且AB=10，一次函数y=x+b与抛物线相交于点E和点F（点E在点F左边），与抛物线的对称轴相交于点G．