题目内容
11. 如图,四边形OACB中,CM⊥OA,∠A+∠B=180°,OA+OB=2OM,CA=CB.求证:OC平分∠AOB.
如图,四边形OACB中,CM⊥OA,∠A+∠B=180°,OA+OB=2OM,CA=CB.求证:OC平分∠AOB.
分析 作CN⊥OB于N,由邻补角定义和已知条件证出∠1=∠A,由AAS证明△BCN≌△ACM,得出CN=CM,即可得出OC平分∠AOB.
解答 证明:作CN⊥OB于N,如图所示: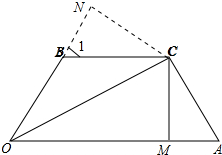
则∠CNB=90°,
∵CM⊥OA,
∴∠CMA=90°=∠CNB,
∵∠A+∠OBC=180°,∠1+∠OBC=180°,
∴∠1=∠A,
在△BCN和△ACM中,$\left\{\begin{array}{l}{∠1=∠A}&{\;}\\{∠CNB=∠CMA}&{\;}\\{CB=CA}&{\;}\end{array}\right.$,
∴△BCN≌△ACM(AAS),
∴CN=CM,
又∵CN⊥OB于N,CM⊥OA于M,
∴OC平分∠AOB.
点评 本题考查了全等三角形的判定与性质、角平分线的判定、邻补角定义;通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
1.下列分式中是最简分式的是( )
| A. | $\frac{{x}^{2}-xy}{2x-xy}$ | B. | $\frac{{x}^{2}-9}{x-3}$ | ||
| C. | $\frac{2}{{x}^{2}-1}$ | D. | $\frac{{x}^{2}+10x+25}{{x}^{2}-25}$ |
 如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?
如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗? 如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:
如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时: