题目内容
9.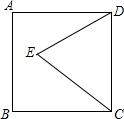 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )| A. | 6 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 过点E作EF⊥CD,利用等边三角形的性质可得DE=EC=CD=6,∠DEF=30°,由直角三角形的性质易得DF,利用勾股定理可得结论.
解答  解:过点E作EF⊥CD,△DCE为等边三角形,
解:过点E作EF⊥CD,△DCE为等边三角形,
∴∠EDC=60°,DE=EC=CD=6,
∵EF⊥CD,
∴∠DEF=30°,
∴DF=$\frac{1}{2}DE$=3,
∴EF=$\sqrt{{DE}^{2}{-DF}^{2}}$=$\sqrt{{6}^{2}{-3}^{2}}$=3$\sqrt{3}$,
故选B.
点评 本题主要考查了等边三角形的性质,正方形的性质及勾股定理,综合利用各性质是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.下列运算错误的是( )
| A. | a4•a3=a7 | B. | a4-a3=a | C. | (a4)3=a12 | D. | (ab)3=a3b3 |
20.下列运算正确的是( )
| A. | y4+y6=y10 | B. | a4+b4=(a+b)4 | C. | a4•a7=a11 | D. | (x3)3=x6 |
1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )
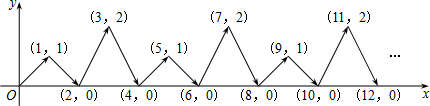

| A. | (2015,0) | B. | (2015,1) | C. | (2015,2) | D. | (2016,0) |
18. 如图,经过平移能得到如图图形的是( )
如图,经过平移能得到如图图形的是( )
 如图,经过平移能得到如图图形的是( )
如图,经过平移能得到如图图形的是( )| A. |  | B. |  | C. |  | D. |  |
19.下列运算正确的是( )
| A. | a+a=2a2 | B. | a2•a=2a2 | C. | (-ab)2=2ab2 | D. | (2a)2÷a=4a |
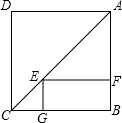 如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E、F.若正方形ABCD的周长是40cm,
如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E、F.若正方形ABCD的周长是40cm,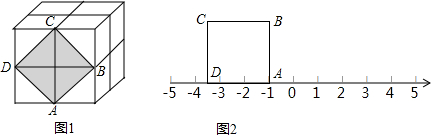
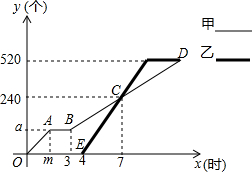 甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.
甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.