题目内容
11.若a、b互为倒数,b、c互为相反数,m的绝对值为$\frac{1}{2}$,求代数式$\frac{ab+(-2b-2c){m}^{2}}{m}$-m2的值.分析 利用倒数,相反数以及绝对值的代数意义求出ab,c+d,m的值,代入原式计算即可得到结果.
解答 解:根据题意得:ab=1,c+d=0,m=$\frac{1}{2}$或-$\frac{1}{2}$,
当m=$\frac{1}{2}$时,原式=$\frac{1+(-2)×0×\frac{1}{4}}{\frac{1}{2}}$-$\frac{1}{4}$=1$\frac{3}{4}$;
当m=-$\frac{1}{2}$时,原式=$\frac{1+(-2)×0×\frac{1}{4}}{-\frac{1}{2}}$$-\frac{1}{4}$=-2$\frac{1}{4}$.
综上所述,代数式$\frac{ab+(-2b-2c){m}^{2}}{m}$-m2的值为1$\frac{3}{4}$或$-2\frac{1}{4}$.
点评 此题考查了代数式求值,相反数,绝对值,以及倒数,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.若直线y=kx+b经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是( )
| A. | y=2x+3 | B. | y=3x+2 | C. | y=-$\frac{2}{3}$x+2 | D. | y=x-1 |
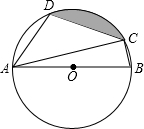 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.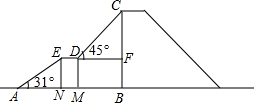 如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)