题目内容
6. 如图,在四边形ABDC中,∠BAC=90°,AB=2,AC=4,E、F分别是BD、CD靠近点D的三等分点,连接AE、AF、EF.若四边形ABDC的面积为7,则△AEF的面积为2.
如图,在四边形ABDC中,∠BAC=90°,AB=2,AC=4,E、F分别是BD、CD靠近点D的三等分点,连接AE、AF、EF.若四边形ABDC的面积为7,则△AEF的面积为2.
分析 连接BC,AD,利用相似三角形的性质和三角形的面积公式进行解答即可.
解答 解:连接BC,AD,如图:
∵∠BAC=90°,AB=2,AC=4,
∴△ABC的面积=$\frac{1}{2}×2×4$=4;
∵四边形ABDC的面积为7,
∴△BDC的面积=7-4=3,
∵E、F分别是BD、CD的三等分点,
∴△EDF的面积=$\frac{1}{9}×3=\frac{1}{3}$,
∵E、F分别是BD、CD的三等分点,
∴△EAD的面积=$\frac{1}{3}△ABD$的面积,△ADF的面积=$\frac{1}{3}$△DAC的面积,
∴△EAD的面积+△DAF的面积=$\frac{1}{3}×$7=$\frac{7}{3}$,
∴△AEF的面积=$\frac{7}{3}-\frac{1}{3}=2$,
故答案为:2
点评 此题考查三角形的面积,关键是利用相似三角形的性质和三角形的面积公式进行解答.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10.下列实数$\sqrt{2}$,-$\root{3}{4}$,0.$\stackrel{..}{32}$,$\frac{22}{7}$,$\frac{π}{3}$,($\sqrt{2}$-1)0,-$\sqrt{9}$,0.1010010001…中,其中非无理数共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
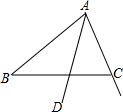 如图,在△ABC中,AB>AC,AD平分∠BAC
如图,在△ABC中,AB>AC,AD平分∠BAC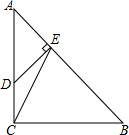 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE.求:
如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE.求: