题目内容
15.已知a=$\frac{-\sqrt{6}-\sqrt{6-4\sqrt{2}}}{2}$,求a3+$\sqrt{6}$a2+$\sqrt{2}$a+$\sqrt{6}$的值.分析 根据a的特点得到a是方程x2+$\sqrt{6}$x+$\sqrt{2}$=0的一个根,把原式因式分解,代入计算即可.
解答 解:a=$\frac{-\sqrt{6}-\sqrt{6-4\sqrt{2}}}{2}$是方程x2+$\sqrt{6}$x+$\sqrt{2}$=0的一个根,
则a2+$\sqrt{6}$a+$\sqrt{2}$=0,
原式=a(a2+$\sqrt{6}$a+$\sqrt{2}$)+$\sqrt{6}$=$\sqrt{6}$.
点评 本题考查的是二次根式的化简,掌握一元二次方程的根的概念是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.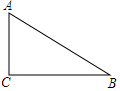 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )| A. | 点B在⊙A外 | B. | 点B在⊙A上 | ||
| C. | 点B在⊙A外内 | D. | 点B与⊙A的位置关系不能确定 |
 如图,在四边形ABDC中,∠BAC=90°,AB=2,AC=4,E、F分别是BD、CD靠近点D的三等分点,连接AE、AF、EF.若四边形ABDC的面积为7,则△AEF的面积为2.
如图,在四边形ABDC中,∠BAC=90°,AB=2,AC=4,E、F分别是BD、CD靠近点D的三等分点,连接AE、AF、EF.若四边形ABDC的面积为7,则△AEF的面积为2.