题目内容
10.下列实数$\sqrt{2}$,-$\root{3}{4}$,0.$\stackrel{..}{32}$,$\frac{22}{7}$,$\frac{π}{3}$,($\sqrt{2}$-1)0,-$\sqrt{9}$,0.1010010001…中,其中非无理数共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 无理数就是无限不循环小数,根据定义即可判断.
解答 解:无理数有$\sqrt{2}$,-$\root{3}{4}$,$\frac{π}{3}$,0.1010010001…,共4个,不是无理数的是0.$\stackrel{..}{32}$,$\frac{22}{7}$,$\frac{π}{3}$,($\sqrt{2}$-1)0,-$\sqrt{9}$共4个.故选C.
点评 本题考查了无理数的定义,无理数常见的三种类型(1)开不尽的方根,如$\sqrt{2}$等.(2)特定结构的无限不循环小数,如0.303 003 000 300 003…(两个3之间依次多一个0).(3)含有π的绝大部分数,如2π.注意:判断一个数是否为无理数,不能只看形式,要看化简结果.如$\sqrt{16}$是有理数,而不是无理数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列等式变形中,结果不正确的是( )
| A. | 如果a=b,那么a+2b=3b | B. | 如果a=3,那么a-k=3-k | ||
| C. | 如果m=n,那么mc2=nc2 | D. | 如果mc2=nc2,那么m=n |
1.大于-2.5,不小于2的整数共有( )个.
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
2.5.24万精确到( )
| A. | 十分位 | B. | 百分位 | C. | 万位 | D. | 百位 |
19.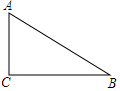 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )| A. | 点B在⊙A外 | B. | 点B在⊙A上 | ||
| C. | 点B在⊙A外内 | D. | 点B与⊙A的位置关系不能确定 |
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2016=22015.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2016=22015.
 如图,在四边形ABDC中,∠BAC=90°,AB=2,AC=4,E、F分别是BD、CD靠近点D的三等分点,连接AE、AF、EF.若四边形ABDC的面积为7,则△AEF的面积为2.
如图,在四边形ABDC中,∠BAC=90°,AB=2,AC=4,E、F分别是BD、CD靠近点D的三等分点,连接AE、AF、EF.若四边形ABDC的面积为7,则△AEF的面积为2.