题目内容

20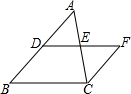．如图，点D、E分别是△ABC的边AB，AC的中点，点F在DE的延长线上，且EF=DE．求证：
（1）BD=FC；
（2）AB∥CF．

分析 （1）可通过证△AED≌△CEF，得出AD=CF，已知AD=BD，由此可证得BD=CF．
（2）由（1）的全等三角形，可得∠ADE=∠CFE，由此可得FC∥AB．

解答 证明：（1）∵E为AC的中点，
∴AE=EC．
在△AED和△CEF中
$\left\{\begin{array}{l}{AE=CE}\\{∠AED=∠CEF}\\{ED=EF}\end{array}\right.$，
∴△AED≌△CEF．
∴AD=CF，
又∵点D为AB的中点，
∴AD=BD，
∴CF=BD；

（2）由（1）知△AED≌△CEF，
∴∠ADE=∠F．
∴FC∥AB．

点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，全等三角形的判定与性质，平行线的判定，熟记定理是解题的关键．

练习册系列答案
相关题目
8．如图，将一副三角板的直角顶点O重叠在一起，若∠AOD=135度，则∠BOC=45度．
9．我们定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad+bc，例如$|\begin{array}{l}{2}&{3}\\{4}&{5}\end{array}|$=2×5+3×4=32．
（1）求$|\begin{array}{l}{0.5}&{3}\\{-2}&{-4}\end{array}|$；
（2）x，y满足$|\begin{array}{l}{x}&{-y}\\{y}&{y}\end{array}|$=3，求2-3xy+3y2的值．
8．用表示大小关系的符号填空：
（1）a2≥0；    
（2）-|x|≤0；
（3）x2+1＞0；       
（4）x2-2xy+y2≥0．
15．【阅读理解】当a＞0，b＞0时，a=（$\sqrt{a}$）2，b=（$\sqrt{b}$）2则（$\sqrt{a}$-$\sqrt{b}$）2=（$\sqrt{a}$）2-2$\sqrt{ab}$+（$\sqrt{b}$）2=a+b-2$\sqrt{ab}$≥0，那么$\frac{a+b}{2}$≥$\sqrt{ab}$，因此对任意两个正数a，b，即a＞0，b＞0，则有下面的不等式；$\frac{a+b}{2}$$≥\sqrt{ab}$，当且仅当a=b时取等号，我们把$\frac{a+b}{2}$叫做正数a，b的算术平均数，把$\sqrt{ab}$叫做正数a，b的几何平均数，于是上述的不等式可以表述为：两个正数的算术平均数不小于（即大于或等于）他们的几何平均数，它在数学中有广泛的应用，是解决最大（小）值问题的有力工具．
【实例剖析】已知x＞0，求式子y=x+$\frac{4}{x}$的最小值．
解：令a=x，b=$\frac{4}{x}$，则由$\frac{a+b}{2}$≥$\sqrt{ab}$，得y=x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=2×$\sqrt{4}$=4，当且仅当x=$\frac{4}{x}$时，即x=2时，式子的最小值，最小值为4．
【学以致用】根据上面的阅读材料回答下列问题：
（1）已知x＞0，则当x为$\frac{\sqrt{6}}{2}$时，式子y=2x+$\frac{3}{x}$取到最小值，最小值是2$\sqrt{6}$．
（2）用篱笆围一个面积为64m2的矩形花园，问这个矩形的长、宽各为多少时，所用的篱笆最短，最短是多少米？
（3）已知x＞0，则当x取何值时，式子y=$\frac{x}{{x}^{2}-2x+9}$取到最大值，最大值是多少？
5．有一种可食用的野生菌，刚上市时，外商李经理以每千克30元的市场价格收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这种野生菌在冷库中最多保存140天，同时，平均每天有3千克的野生菌损坏导致不能出售．李经理将这批野生菌存放多少天后一次性全部出售可以获得22500元的利润？
12．计算：（-3）2017•（-$\frac{1}{3}}$）2016=-3．
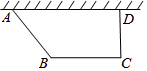9．如图，要建造一个直角梯形的花圃，要求AD边靠墙，CD⊥AD，AB：CD=5：4，另外三边的和为20米，设AB的长为5x米
（1）求出AD的长；（用含字母x的式子表示）
（2）若该花圃的面积为50平方米，且周长不大于30米，求AB的长．
10．已知xa+a=3是关于x的一元一次方程，则该方程的解为（　　）
A．x=1B．x=2C．x=3D．x=4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网