题目内容
17.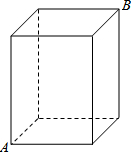 如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处,蚂蚁爬行的最短路程是100cm.
如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处,蚂蚁爬行的最短路程是100cm.
分析 蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.
解答 解:第一种情况:如图1,把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是90cm和50cm,
则所走的最短线段AB=$\sqrt{5{0}^{2}+9{0}^{2}}$=10$\sqrt{106}$cm;
第二种情况:如图2,把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是110cm和30cm,
所以走的最短线段AB=$\sqrt{11{0}^{2}+3{0}^{2}}$=10$\sqrt{130}$cm;
第三种情况:如图3,把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是80cm和60cm,
所以走的最短线段AB=$\sqrt{8{0}^{2}+6{0}^{2}}$=100cm;
三种情况比较而言,第三种情况最短.
故答案为:100cm.
点评 本题考查了立体图形中的最短路线问题;通常应把立体几何中的最短路线问题转化为平面几何中的求两点间距离的问题;注意长方体展开图形应分情况进行探讨.

练习册系列答案
相关题目
2.下列调查中,适合普查的是( )
| A. | 了解某文稿的错别字情况 | B. | 了解某种灯泡的使用寿命情况 | ||
| C. | 了解某市学生的视力情况 | D. | 了解某市老年人参加晨练的情况. |
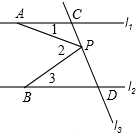 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点.有一点P在C,D之间运动(不与C,D两点重合),在它运动的过程中,∠1+∠3=∠2这一相等关系是否始终成立?试说明理由.
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点.有一点P在C,D之间运动(不与C,D两点重合),在它运动的过程中,∠1+∠3=∠2这一相等关系是否始终成立?试说明理由. 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,求证:四边形ABCD是正方形.
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,求证:四边形ABCD是正方形.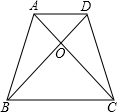 如图:在梯形ABCD中两条对角线AC、BD相交于点O,已知OB=18cm,OD=12cm,则S△ABD:S△ABC=$\frac{2}{3}$.
如图:在梯形ABCD中两条对角线AC、BD相交于点O,已知OB=18cm,OD=12cm,则S△ABD:S△ABC=$\frac{2}{3}$.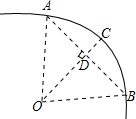 如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )
如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )