题目内容
12.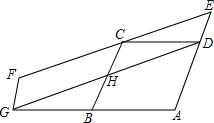 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 由AAS证明△CDH≌△BGH,得出CH=BH=$\frac{1}{2}$BC=$\frac{1}{2}$AD,DH=GH,得出△CDH的面积=△BGH的面积=$\frac{1}{4}$平行四边形ABCD的面积,得出四边形ABHD的面积=$\frac{3}{4}$平行四边形ABCD的面积,再证出平行四边形ABCD的面积=平行四边形DEFG的面积,即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,BC=AD,
∴∠CDH=∠BGH,
∵B为AG中点,
∴BG=AB,
∴CD=BG,
在△CDH和△BGH中,
$\left\{\begin{array}{l}{∠CDH=∠BGH}&{\;}\\{∠CHD=∠BHG}&{\;}\\{CD=BG}&{\;}\end{array}\right.$,
∴△CDH≌△BGH(AAS),
∴CH=BH=$\frac{1}{2}$BC=$\frac{1}{2}$AD,DH=GH,
∴△BGH的面积=$\frac{1}{4}$△AGD的面积,
∴△CDH的面积=△BGH的面积=$\frac{1}{4}$平行四边形ABCD的面积,
∴四边形ABHD的面积=$\frac{3}{4}$平行四边形ABCD的面积,
∵四边形DEFG是平行四边形,
∴FG∥ED,EF∥CD,FG=ED,
∴四边形DECH是平行四边形,
∴ED=CH=$\frac{1}{2}$AD,
∴FG=$\frac{1}{2}$AD,
∴平行四边形ABCD的面积=平行四边形DEFG的面积,
∴$\frac{{S}_{1}}{{S}_{2}}=\frac{3}{4}$;
故选:C.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、三角形和四边形面积的关系;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案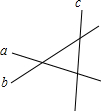 如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
| A. | x<1 | B. | x≥1 | C. | x≤-1 | D. | x<-1 |
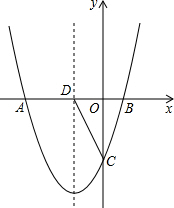 如图,抛物线y1=$\frac{1}{2}$x2+bx+c与x轴交于点A、B,交y轴于点C(0,-2$\sqrt{3}$),且抛物线对称轴x=-2交x轴于点D,E是抛物线在第3象限内一动点.
如图,抛物线y1=$\frac{1}{2}$x2+bx+c与x轴交于点A、B,交y轴于点C(0,-2$\sqrt{3}$),且抛物线对称轴x=-2交x轴于点D,E是抛物线在第3象限内一动点. 如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,直角△CEF的面积为200,则BE的值为12.
如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,直角△CEF的面积为200,则BE的值为12.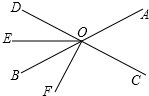 如图,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
如图,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°. 读如图提供的信息,回答下列问题.
读如图提供的信息,回答下列问题.