题目内容
20.设a*b=($\frac{1}{a}-\frac{1}{b}$)+ab,求:(1)-2*3
(2)[1*(-2)*4].
分析 (1)利用新运算的定义求解即可;
(2)利用新运算的定义顺次求解即可.
解答 解:(1)∵a*b=($\frac{1}{a}-\frac{1}{b}$)+ab,
∴-2*3=(-$\frac{1}{2}$-$\frac{1}{3}$)+(-2)•3=-$\frac{5}{6}$-6=-6$\frac{5}{6}$,
(2)[1*(-2)*4]
=[1+$\frac{1}{2}$+1×(-2)]*4
=(-$\frac{1}{2}$)*4
=(-2-$\frac{1}{4}$)+(-2)
=-4$\frac{1}{4}$.
点评 本题主要考查了有理数的混合运算,解题的关键是理解新运算的定义.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
12.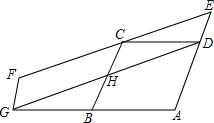 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
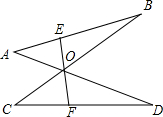 如图,AD、BC相交于点O,且OA=OC,OB=OD,EF过点O,分别交AB、CD于点E、F,且∠AOE=∠COF,求证:OE=OF.
如图,AD、BC相交于点O,且OA=OC,OB=OD,EF过点O,分别交AB、CD于点E、F,且∠AOE=∠COF,求证:OE=OF. 有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米).另三边用竹篱笆围成,如果竹篱笆的全长为34米.且开有一个1米宽的小门.问鸡场的长和宽各为多少?
有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米).另三边用竹篱笆围成,如果竹篱笆的全长为34米.且开有一个1米宽的小门.问鸡场的长和宽各为多少?