题目内容
17.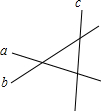 如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
分析 由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
解答 解:∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件; 如图:点P是△ABC两条外角平分线的交点,
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选D.
点评 此题考查了角平分线的性质.注意掌握角平分线上的点到角两边的距离相等,注意数形结合思想的应用,小心别漏解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
12.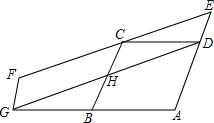 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
2. 如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
 如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )| A. | 2 | B. | 3 | C. | 6 | D. | 8 |
9.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)【方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]】
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分越高成绩越好,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.请问A同学的数学成绩好还是英语成绩好?
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | $\sqrt{2}$ | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分越高成绩越好,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.请问A同学的数学成绩好还是英语成绩好?
6.要使六边形木架不变形,至少要再钉上( )根木条.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
7.将△ABC三个顶点横坐标都乘以-1,纵坐标不变,则所得图形与原图形的关系是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 不存在对称关系 |