题目内容
4.下列命题:①方程x2=x的解是x=1
②4的平方根是2;
③有两边和一角相等的两个三角形全等;
④连接任意四边形各边中点的四边形是平行四边形;
其中是真命题的有( )个.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 通过解一元二次方程可对①进行判断;根据平方根的定义对②进行判断;根据全等三角形的判定方法对③进行判断;根据三角形中位线和平行四边形的性质对④进行判断.
解答 解:方程x2=x的解是x1=1,x2=0,所以①错误;
4的平方根是±2,所以②错误;
有两边和它们的夹角对应相等的两个三角形全等,所以③错误;
连接任意四边形各边中点的四边形是平行四边形,所以④正确.
故选D.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
相关题目
12.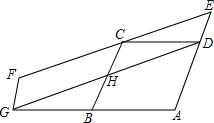 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
 如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,B为AG中点,四边形ABCD和四边形DEFG均为平行四边形,C为EF上一点,若四边形ABHD和四边形DEFG的面积分别为S1和S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
9.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)【方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]】
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分越高成绩越好,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.请问A同学的数学成绩好还是英语成绩好?
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | $\sqrt{2}$ | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分越高成绩越好,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.请问A同学的数学成绩好还是英语成绩好?
13.在某次体育测试中,九年级(1)班7名女同学一分钟仰卧起坐的成绩(单位:个)分别为22,24,30,26,28,23,24,则这组数据的众数和中位数分别是( )
| A. | 24,24 | B. | 26,24 | C. | 28,26 | D. | 30,26 |
14.我们学习解二元一次方程组时,通过代入消元法或者加减消元法变二元方程为一元方程,这种解题方法主要体现的数学思想是( )
| A. | 分类讨论 | B. | 化归与转化 | C. | 函数与方程 | D. | 数形结合 |