题目内容
17.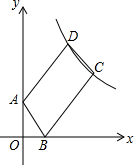 如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.
如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.
分析 由A(0,2),B(1,0),计算出AB=$\sqrt{(1-0)^{2}+(0-2)^{2}}$=$\sqrt{5}$,由AB=$\frac{1}{2}$BC,得出BC=2AB=2$\sqrt{5}$.设D(x,y),根据点D在双曲线上得到xy=k.根据平移的性质得出C(x+1,y-2),那么(x+1)(y-2)=k.根据题意,列出方程组$\left\{\begin{array}{l}{{x}^{2}+(y-2)^{2}=20①}\\{xy=(x+1)(y-2)②}\end{array}\right.$,求解即可.
解答 解:∵A点坐标为(0,2),B点坐标为(1,0),
∴AB=$\sqrt{(1-0)^{2}+(0-2)^{2}}$=$\sqrt{5}$,
∵AB=$\frac{1}{2}$BC,
∴BC=2AB=2$\sqrt{5}$.
设D(x,y),则xy=k.
∵将AB沿BC方向从B平移到C,点A的对应点为D,
∴C(x+1,y-2),则(x+1)(y-2)=k.
根据题意,得$\left\{\begin{array}{l}{{x}^{2}+(y-2)^{2}=20①}\\{xy=(x+1)(y-2)②}\end{array}\right.$,
由②得,y=2x+2③,
把③代入①,解得x=±2(负值舍去),
∴x=2,此时y=6,
∴k=2×6=12.
故答案为12.
点评 本题考查了反比例函数图象上点的坐标特征,两点间的距离公式,坐标与图形变化-平移等知识,设D(x,y),根据平移的性质得出C点坐标为(x+1,y-2),是解题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
5.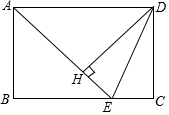 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.滴滴快车是一种便捷的出行工具,计价规则如下表:
小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里.如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差( )
| 计费项目 | 里程费 | 时长费 | 远途费 |
| 单价 | 1.8元/公里 | 0.3元/分钟 | 0.8元/公里 |
| 注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元. | |||
| A. | 10分钟 | B. | 13分钟 | C. | 15分钟 | D. | 19分钟 |
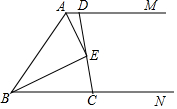 如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求:
如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求:
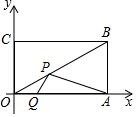 已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).
已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).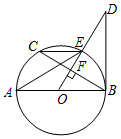 如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.