题目内容
14.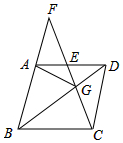 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:△ADG≌△CDG.
(2)求证:CE=3,EF=4,求AG的长.
分析 (1)根据菱形的性质得到AB∥CD,AD=CD,∠ADB=∠CDB,推出△ADG≌△CDG,根据全等三角形的性质即可得到结论;
(2)由全等三角形的性质得到∠EAG=∠DCG,等量代换得到∠EAG=∠F,求得△AEG∽△FGA,即可得到结论.
解答 解:(1)∵四边形ABCD是菱形,
∴AB∥CD,AD=CD,∠ADB=∠CDB,
∴∠F=∠FCD,
在△ADG与△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADG=∠CDG}\\{DG=DG}\end{array}\right.$,
∴△ADG≌△CDG,
∴∠EAG=∠DCG,
∴AG=CG;
(2)∵△ADG≌△CDG,
∴∠EAG=∠F,
∵∠AGE=∠AGE,
∴△AGE∽△FGA,
∴$\frac{AG}{FG}$=$\frac{GE}{AG}$,
∴AG2=GE•GF,设AG=CG=x,
则有x2=(3-x)(7-x),
解得x=2.1,
∴AG=2.1.
点评 本题考查了相似三角形的判定和性质,菱形的性质,全等三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
5.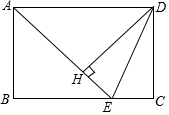 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.已知双曲线y=$\frac{k}{x}$经过点(m,n),(n+1,m-1),(m2-1,n2-1),则k的值为( )
| A. | 0或3 | B. | 0或-3 | C. | -3 | D. | 3 |
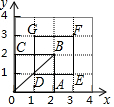 如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移$\frac{1}{2}$OB个单位,则点C的对应点坐标为(1,3).
如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移$\frac{1}{2}$OB个单位,则点C的对应点坐标为(1,3).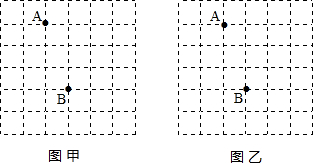
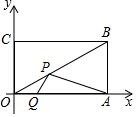 已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).
已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).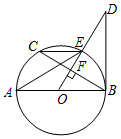 如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.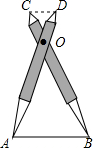 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )