题目内容
9.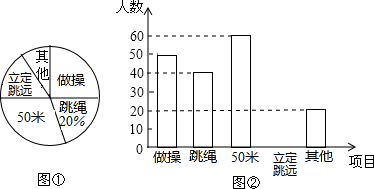 为了解某校八年级学生参加体育活动情况,从该校八年级学生中随机抽取了部分学生的体育活动自选项目进行统计,并根据调查结果绘制了如下两个统计图,请根据图中信息,回答下列问题:(1)本次调查共抽取了200名学生;
为了解某校八年级学生参加体育活动情况,从该校八年级学生中随机抽取了部分学生的体育活动自选项目进行统计,并根据调查结果绘制了如下两个统计图,请根据图中信息,回答下列问题:(1)本次调查共抽取了200名学生;(2)在条形统计图中,请把空缺部分补充完整;
(3)该校共有八年级学生860名,估计该校八年级选报做操项目的学生人数.
分析 (1)根据题意,结合选报跳绳的人数与其所占的百分比,计算可得本次调查共抽取的学生数;
(2)读图并计算,可得参加立定跳远的人数为200-20-40-50-60=30,补充完整即可;
(3)首先计算出样本中选报做操的百分比,继而估计报做操的学生数.
解答 解:(1)40÷20%=200(人),
故答案为:200;
(2)立定跳远的人数为:200-50-40-60-20=30(人)
如图,
(3)860×$\frac{50}{200}$=215(名)
答:估计该校八年级选报做操项目的学生人数为215名.
点评 本题考查了扇形统计图及条形统计图的知识,此题主要考查学生读图获取信息的能力.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
19.如图是某市某中学八年级(1)班学生参加音乐、美术、体育课外兴趣小组人数的部分条形统计图和扇形统计图,则下列说法错误的是( )
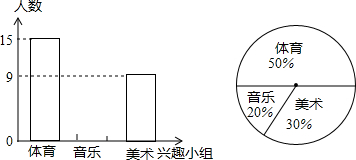

| A. | 八年级(1)班参加这三个课外兴趣小组的学生总人数为30人 | |
| B. | 在扇形统计图中,八年级(1)班参加音乐兴趣小组的学生人数所占的圆心角度数为82° | |
| C. | 八年级(1)班参加音乐兴趣小组的学生人数为6人 | |
| D. | 若该校八年级参加这三个兴趣小组的学生共有200人,那么估计全年级参加美术兴趣小组的学生约有60人 |
17.某工程队准备修建一条长1200米的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前两天完成任务,若设原计划每天修建道路x米,则根据题意可列方程为( )
| A. | $\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=2 | B. | $\frac{1200}{(1-20%)x}$-$\frac{1200}{x}$=2 | ||
| C. | $\frac{1200}{(1+20%)x}$-$\frac{1200}{x}$=2 | D. | $\frac{1200}{x}$-$\frac{1200}{(1-20%)x}$=2 |
14.如果把分式$\frac{xy}{x+y}$中的x和y都扩大为原来的2倍,那么分式的值( )
| A. | 扩大为原来的4倍 | B. | 扩大为原来的2倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{2}$ |
 如图,直线AB,CD相交于O,射线OM平分∠AOC,若∠BOD=80°,求∠BOM的度数.
如图,直线AB,CD相交于O,射线OM平分∠AOC,若∠BOD=80°,求∠BOM的度数.