二次根式$\sqrt{{a}^{2}+{b}^{2}}$.$\sqrt{2{b}^{3}}$.$\sqrt{\frac{a}{2}}$.4$\sqrt{3a}$.$\sqrt{8}$.$\sqrt{0.2}$中.最简二次根式有( )A．1个B．2个C．3个D．4个题目和参考答案——青夏教育精英家教网—

题目内容

2．二次根式$\sqrt{{a}^{2}+{b}^{2}}$，$\sqrt{2{b}^{3}}$，$\sqrt{\frac{a}{2}}$，4$\sqrt{3a}$，$\sqrt{8}$，$\sqrt{0.2}$中，最简二次根式有（　　）

A．

1个

B．

2个

C．

3个

D．

4个

分析检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．

解答解：$\sqrt{{a}^{2}+{b}^{2}}$，4$\sqrt{3a}$是最简二次根式，
故选：B．

点评本题考查最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．

练习册系列答案

学生成长册系列答案

学练案自助读本系列答案

学力水平同步检测与评估系列答案

花山小状元学科能力达标初中生100全优卷系列答案

金考卷百校联盟高考考试大纲调研卷系列答案

相关题目

15．

如图，a∥b，∠1=70°，则∠2等于（　　）

13．已知x²-3x-4=0，则代数式$\frac{x}{{x}^{2}-x-4}$的值是$\frac{1}{2}$．

10．下列命题中，真命题的个数有（　　）
①对角线互相平分的四边形是平行四边形；②两组对角分别相等的四边形是平行四边形；③一组对边平行，另一组对边相等的四边形是平行四边形；④对角线相等的四边形是矩形．

17．（1）已知方程组$\left\{\begin{array}{l}ax+5y=15----（1）\\ 4x-by=-2---（2）\end{array}\right.$，由于甲看错了方程①中的a得到方程组的解为$\left\{\begin{array}{l}x=-13\\ y=-1\end{array}\right.$，乙看错了方程②中的b得到方程组的解为$\left\{\begin{array}{l}x=5\\ y=4\end{array}\right.$，若按正确的a、b计算，则原方程组的解x与y的差x-y的值是多少？
（2）已知实数x、y、z满足x+y=4及xy=z²+4，则x-y+2z的值为0．

7．以方程组$\left\{\begin{array}{l}{2x+y=t-1}\\{x-y=2t+7}\end{array}\right.$ 的解x、y分别作为某个点的横、纵坐标，得到一个点（x，y），若点（x，y）在第四象限，则t的取值范围是（　　）

14．抛物线y=（3一k）x²+（k-2）x+2k-1（k≠3）过定点，并求出定点的坐标．

11．点P₁（-2，y₁），点P₂（3，y₂）是一次函数y=-4x+m图象上的两个点，则y₁与y₂的大小关系是（　　）

y₁＞y₂

y₁＞y₂＞0

y₁＜y₂

y₁=y₂

12．

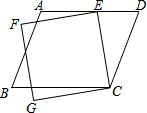如图，有一平行四边形ABCD与一正方形CEFG，其中E点在AD上，若∠ECD=35°，∠AEF=15°，则∠B的度数为70度．

试题分类