题目内容
9.已知2x2-ax-2=0,给出下列结论:①当x=2时,a+$\frac{1}{a}$=$\frac{10}{3}$;②若a=1时,2x2+$\frac{2}{{x}^{2}}$=6;③若a=2时,x3-4x2+2x=-3,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
分析 ①把x=2代入方程中,可得x=3,所以a+$\frac{1}{a}$=$\frac{10}{3}$;
②先将a=1代入原方程,再进行变形为:x-$\frac{1}{x}$=$\frac{1}{2}$,两边平方可得结论;
③先将a=2代入原方程,变形后得:x3=x2+x,x2-x=1,分别代入所求代数式达到降次的目的,可得结论.
解答 解:①当x=2时,2×4-2a-2=0,
a=3,
∴a+$\frac{1}{a}$=3+$\frac{1}{3}$=$\frac{10}{3}$;
所以选项①正确;
②当a=1时,2x2-x-2=0,
两边同时除以x,得,
2x-1-$\frac{2}{x}$=0,
2x-$\frac{2}{x}$=1,
x-$\frac{1}{x}$=$\frac{1}{2}$,
两边同时平方得:x2-2+$\frac{1}{{x}^{2}}$=$\frac{1}{4}$,
两边同时乘以2得:2x2+$\frac{2}{{x}^{2}}$-4=$\frac{1}{2}$,
∴2x2+$\frac{2}{{x}^{2}}$=4+$\frac{1}{2}$=$\frac{9}{2}$≠6;
所以选项②不正确;
③当a=2时,2x2-2x-2=0,
∴x2-x-1=0,x2-x=1,
两边同时乘以x,得:x3-x2-x=0,
x3=x2+x,
∴x3-4x2+2x=x2+x-4x2+2x=-3x2+3x=-3(x2-x)=-3,
所以选项③正确;
故选D.
点评 本题考查了完全平方公式和整体代入的运用,熟练掌握完全平方公式是做好本题的关键.

练习册系列答案
相关题目
 已知线段AB=6cm,延长AB至点C,使BC=AB,反向延长线段AB至D,使AD=AB.
已知线段AB=6cm,延长AB至点C,使BC=AB,反向延长线段AB至D,使AD=AB.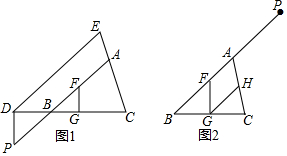
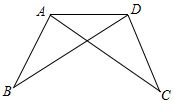 如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.
如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.