题目内容
2．
如图，在△ABC中，AC=AB，底边BC=10，点D是腰AB上一点，且CD=8，BD=6，求△ABC的周长．
分析 直接利用勾股定理的逆定理得出△BDC是直角三角形，再结合勾股定理得出AC的长，即可得出答案．
解答 解：∵BC=10，CD=8，BD=6，
∴BD2+DC2=BC2，
∴△BDC是直角三角形，
∵AB=AC，
∴设AC=x，则AD=x-6，
∴x2=（x-6）2+82，
解得：x=$\frac{25}{3}$，
故AB=AC=$\frac{25}{3}$，
则△ABC的周长为：10+$\frac{50}{3}$=$\frac{80}{3}$．
点评 此题主要考查了勾股定理以及勾股定理的逆定理，正确得出AC的长是解题关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6．已知△ABC的三个顶点A（5，6）、B（7，2）、C（4，3），先将△ABC向左平移一个单位，再以原点O为位似中心，在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段△A′B′C′，则点A的对应点A′的坐标为（ ）
| A． | （2，1） | B． | （3，1） | C． | （2，3） | D． | （3，3） |
7．在△ABC中，∠A=90°，AB=6，AC=8，AD是BC边上的高，CD的长是（ ）
| A． | 6.4 | B． | 6 | C． | 5.6 | D． | 10 |
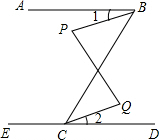如图，已知∠ABC+∠ECB=180°，∠P=∠Q，则∠1与∠2是否相等？说说你的理由．
11．
下列图中，与图中由实线围成的图形成全等形的是（ ）
下列图中，与图中由实线围成的图形成全等形的是（ ）| A． |  | B． |  | C． |  | D． |  |
