题目内容
3.计算:(1)$\sqrt{27}$-($\sqrt{5}$)0+$\frac{\sqrt{12}}{\sqrt{3}}$;
(2)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$;
(3)(2+$\sqrt{3}$)(2-$\sqrt{3}$)-($\sqrt{2}$+1)2.
分析 (1)化简二次根式、计算零指数幂、二次根式的除法,再计算加减即可;
(2)先化简括号内的二次根式、将除法转化为乘法,再用乘法分配律展开分别计算即可得;
(3)先用平方差和完全平方公式展开,再去括号计算加减即可.
解答 解:(1)原式=$3\sqrt{3}-1+2$=$3\sqrt{3}+1$;
(2)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)×$\frac{1}{2\sqrt{3}}$=$3-\frac{1}{3}+2$=$\frac{14}{3}$;
(3)原式=$4-3-(2+2\sqrt{2}+1)$=$-2-2\sqrt{2}$.
点评 本题主要考查二次根式的混合运算,熟练掌握二次根式的性质化简各二次根式与二次根式的混合运算顺序、完全平方公式、平方差公式是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
11.已知△ABC的顶点的坐标分别是A(-4,0),B(-3,2),C(-1,1),△ABC与△A1B1C1关于y轴对称,请画出一个平面直角坐标系,并在该平面直角坐标系上画出△ABC及△A1B1C1.
18.下面运算正确的是( )
| A. | ${(\frac{1}{2})}^{-1}$=-$\frac{1}{2}$ | B. | (2a)2=2a2 | C. | x2+x2=x4 | D. | |a|=|-a| |
12.已知等腰三角形的一个内角为70°,则另外两个角的度数为( )
| A. | 55°,55° | B. | 55°,70° | ||
| C. | 70°,40° | D. | 55°,55°或70°,40° |
13.计算(-5)÷(-2)=( )
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | $\frac{2}{5}$ |
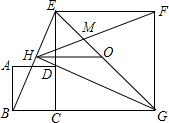 如图,正方形ABCD的边与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE②HO$\frac{∥}{=}$$\frac{1}{2}$BG;③GH2=GM•GE;④△GBE∽△GMF,其中正确的有( )
如图,正方形ABCD的边与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE②HO$\frac{∥}{=}$$\frac{1}{2}$BG;③GH2=GM•GE;④△GBE∽△GMF,其中正确的有( )