题目内容
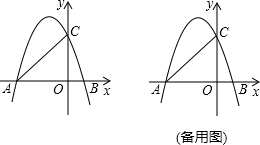
8.如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC,把△ABC沿x轴向右平移得到△A′B′C′,AB边上的点O平移到点O′.(1)求点B、C的坐标及抛物线的对称轴;
(2)在平移的过程中,设点B关于直线A′C′的对称点为点F,当点F落在直线AC上时,求△ABC平移的距离;
(3)在平移过程中,连接CA′,CO′,求△A′CO′周长的最小值.
分析 (1)通过解方程$\frac{3}{4}$x2-$\frac{9}{4}$x+3=0可得A点和B点坐标,再计算自变量为0时的函数值可得到C点坐标,然后利用对称性可确定抛物线的对称轴;
(2)根据轴对称的性质对称BM=FM,由平移的定义可知A′M∥AC,根据平行线分线段成比例定理即可证得AA′=BA′=$\frac{5}{2}$,从而求得平移的距离为$\frac{5}{2}$;
(3)过A点作AN⊥x轴,且AN=OC,易证得△NAA′≌△COO′,得出A′N=CO′,根据两点之间线段最短,当△A′CO′周长的最小时,A′在直线NC上,即∠AA′N=∠CA′O,即可根据AAS证得△NAA′≌△COA′,得出AA′=OA′,NA′=NA′,然后根据勾股定理求得CA′=$\sqrt{13}$,即可求得三角形周长的最小值.
解答  解:(1)当y=0时,-$\frac{3}{4}$x2-$\frac{9}{4}$x+3=0,解得x1=1,x2=-4,则A(-4,0),B(1,0),
解:(1)当y=0时,-$\frac{3}{4}$x2-$\frac{9}{4}$x+3=0,解得x1=1,x2=-4,则A(-4,0),B(1,0),
当x=0时,y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3=3,则C(0,3);
抛物线的对称轴是直线x=$\frac{-4+1}{2}$=-$\frac{3}{2}$;
(2)∵点B和点F关于直线A′C′的对称,
∴BM=FM,
由平移的定义可知A′M∥AC,
∴$\frac{BA′}{AA′}$=$\frac{BM}{FM}$=1,
∴AA′=BA′=$\frac{1}{2}$AB,
∵A(-4,0),B(1,0),
∴AB=5,
∴AA′=BA′=$\frac{5}{2}$,
∴△ABC平移的距离为$\frac{5}{2}$;
(3)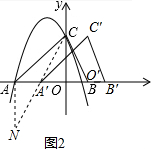 过A点作AN⊥x轴,且AN=OC,
过A点作AN⊥x轴,且AN=OC,
∴∠NAA′=∠COO′=90°,
在△NAA′和△COO′中,
$\left\{\begin{array}{l}{AN=CO}\\{∠NAA′=COO′}\\{AA′=OO′}\end{array}\right.$
∴△NAA′≌△COO′(ASA),
∴A′N=CO′,
当△A′CO′周长的最小时,A′在直线NC上,
即∠AA′N=∠CA′O,
在△NAA′和△COA′中,
$\left\{\begin{array}{l}{∠AA′N=∠CA′O}\\{∠NAA′=∠COA′}\\{AN=OC}\end{array}\right.$
∴△NAA′≌△COA′(AAS),
∴AA′=OA′,NA′=NA′,
∴CA′=CO′,
∵OA=4,
∴AA′=OA′=2,
∴OO′=2,
∴A′O′=4,
∵OC=3,
∴CA′=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴△A′CO′周长的最小值为4+2$\sqrt{13}$.
点评 本题是二次函数的综合题,考查了二次函数的性质,轴对称的性质,平行线分线段成比例定理,勾股定理的运用以及三角形全等的判定和性质,(3)能够判断当△A′CO′周长的最小时,A′在直线NC上是本题的难点.

| A. | 各边相等的多边形是正多边形 | B. | 同角或等角的余角相等 | ||
| C. | 必然事件发生的概率为0 | D. | 六边形的内角和等于540° |
| A. | 6.22×104亿 | B. | 0.622×105亿 | C. | 6.22×105亿 | D. | 62.2×103亿 |
| A. | 2×1010 | B. | 2×109 | C. | 20×108 | D. | 2×107 |
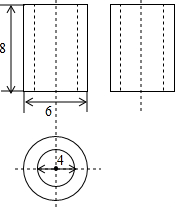 如图是某几何体的三视图,根据图中数据,可得该几何体的体积为( )
如图是某几何体的三视图,根据图中数据,可得该几何体的体积为( )| A. | 9π | B. | 40π | C. | 20π | D. | 16π |
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |