题目内容
16.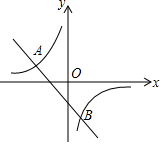 如图,已知A(n,2)、B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(n,2)、B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.(1)求m、n的值;
(2)观察图象,直接写出kx<$\frac{m}{x}$-b的解集;
(3)若将反比例函数y=$\frac{m}{x}$的图象先向下平移1个单位长度,再向右平移4个单位长度,此时该函数图象与x轴、y轴分别交P、Q两点.
①请你直接写P,Q的坐标:P(-4,0)、Q(0,1).
②求四边形APBQ的面积.
分析 (1)把A(n,2),B(2,-4)代入反比例函数y=$\frac{m}{x}$,运用待定系数法求其解析式;
(2)看在交点的哪侧,对于相同的自变量,一次函数小于反比例函数的函数值;
(3)①根据平移规律:加左减右、加上减下得出平移后解析式,分别秀出y=0和x=0时x、y的值可得点P、Q的坐标;
②先求得直线PB解析式得出其与y轴的交点坐标,求出S梯形APCQ、S△BCQ,从而得出答案.
解答 解:(1)∵B(2,-4)在函数y=$\frac{m}{x}$的图象上,
∴m=-8.
∴反比例函数的解析式为:y=-$\frac{8}{x}$.
∵点A(n,2)在函数y=-$\frac{8}{x}$的图象上
∴n=-4;
(2)由交点坐标和图象可知,当-4<x<0或x>2取何值时,kx+b<$\frac{m}{x}$,即kx<$\frac{m}{x}$-b.
(3)①如图,
平移之后的函数解析式为y=-$\frac{8}{x-4}$-1,
当x=0时,y=1,则点Q坐标为(0,1);
当y=0时,-$\frac{8}{x-4}$-1=0,解得x=-4,则点P的坐标为(-4,0),
故答案为:P(-4,0)、Q(0,1);
②设PB交y轴于C点,
设PB的解析式为y=kx+b.
将P、Q坐标代入求得k=-$\frac{2}{3}$,b=-$\frac{8}{3}$.
解析式为y=-$\frac{2}{3}$x-$\frac{8}{3}$.
∴C(0,-$\frac{8}{3}$).
∴S梯形APCQ=$\frac{1}{2}$×(2+$\frac{11}{3}$)×4=$\frac{34}{3}$,S△BCQ=$\frac{1}{2}$×$\frac{11}{3}$×2=$\frac{11}{3}$.
∴S四边形APBQ=15.
点评 此题主要考查了反比例函数与一次函数的交点问题,掌握用待定系数法确定反比例函数的比例系数k,求出函数解析式;同时间接考查函数的增减性来解不等式及四边形的面积问题、平移的规律是解题的关键.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案 如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )
如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )| A. | $y=\frac{{\sqrt{3}}}{5}x+5$ | B. | $y=\sqrt{3}x+5$ | C. | $y=\sqrt{3}x-5$ | D. | $y=-\frac{{\sqrt{3}}}{3}x+5$ |
| A. | (x+2)(x-2)=x2-4 | B. | x2-2x+1=(x-1)2 | C. | a2-2a+2=(a-1)2+1 | D. | 4a2-8a=2a(2a-4) |

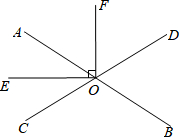 如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.