Question

8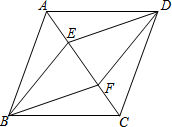．如图，在四边形ABCD中，AB∥CD，点E、F在对角线AC上，且∠ABF=∠CDE，
AE=CF．
（1）求证：△ABF≌△CDE；
（2）当四边形ABCD满足什么条件时，四边形BFDE是菱形？为什么？

Answer 1

分析 （1）由平行线的性质得出∠BAC=∠DCA．证出AF=CE．由AAS证明△ABF≌△CDE即可；
（2）先证明四边形ABCD是菱形，得出BD⊥AC，再证明四边形BFDE是平行四边形，即可得出结论．

解答 （1）证明：∵AB∥CD，
∴∠BAC=∠DCA．
∵AE=CF，
∴AE+EF=CF+EF，即AF=CE．
在△ABF和△CDE中，
$\left\{\begin{array}{l}{∠BAC=∠DCA}&{\;}\\{∠ABF=∠CDE}&{\;}\\{AF=CE}&{\;}\end{array}\right.$，
又∵∠ABF=∠CDE，
∴△ABF≌△CDE（AAS）；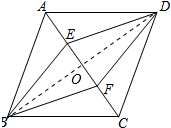
（2）解：当四边形ABCD满足AB=AD时，四边形BEDF是菱形．理由如下：
连接BD交AC于点O，如图所示：
由（1）得：△ABF≌△CDE，
∴AB=CD，BF=DE，∠AFB=∠CED，
∴BF∥DE．
∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形．
又∵AB=AD，
∴平行四边形ABCD是菱形．
∴BD⊥AC．
∵BF=DE，BF∥DE，
∴四边形BEDF是平行四边形，
∴四边形BEDF是菱形．

点评 本题考查了平行线的性质、平行四边形的判定、菱形的判定与性质、全等三角形的判定与性质；熟练掌握菱形的判定与性质，证明三角形全等是解决问题的关键．