题目内容
9.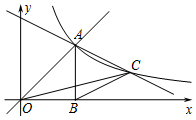 如图,直线y=x与反双曲线y=$\frac{k}{x}$(k>0)在第一象限交于点A,AB⊥x轴于B(2,0),点C是双曲线y=$\frac{k}{x}$(k>0)图象上一动点.
如图,直线y=x与反双曲线y=$\frac{k}{x}$(k>0)在第一象限交于点A,AB⊥x轴于B(2,0),点C是双曲线y=$\frac{k}{x}$(k>0)图象上一动点.(1)求反比例函数的解析式.
(2)①若△OBC的面积为1,求△AOC的面积.
②在①的条件下,根据图象直接写出在第一象限内当x满足什么条件时,经过点A、C的一次函数的函数值小于反比例函数y=$\frac{k}{x}$的函数值.
分析 (1)根据点A的横坐标为2,即可得到A(2,2),再代入双曲线y=$\frac{k}{x}$,可得反比例函数的解析式.
(2)①过C作CD⊥x轴于D,根据△OBC的面积为1,求得CD=1,进而得到C(4,1),再根据S△AOC+S△COD=S△AOB+S四边形ABDC,即可得到△AOC的面积.
②根据在第一象限内经过点A、C的一次函数的函数值小于反比例函数y=$\frac{k}{x}$的函数值,即可得到x的取值范围.
解答 解:(1)∵AB⊥x轴于B(2,0),
∴点A的横坐标为2,
在直线y=x中,当x=2时,y=2,
∴A(2,2),
把A(2,2)代入双曲线y=$\frac{k}{x}$,可得
k=2×2=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
(2)①如图,过C作CD⊥x轴于D,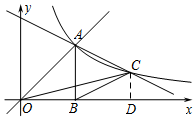
当△OBC的面积为1时,$\frac{1}{2}$OB×CD=1,
∴$\frac{1}{2}$×2×CD=1,即CD=1,
当y=1时,1=$\frac{4}{x}$,
∴x=4,即C(4,1),
∵S△AOC+S△COD=S△AOB+S四边形ABDC,
∴S△AOC+$\frac{1}{2}$|4|=$\frac{1}{2}$|4|+$\frac{(1+2)×2}{2}$,
∴S△AOC=3;
②由图可得,第一象限内,当x满足:0<x<2或x>4时,经过点A、C的一次函数的函数值小于反比例函数y=$\frac{k}{x}$的函数值.
点评 本题主要考查了一次函数与反比例函数交点问题,反比例函数与一次函数的交点问题,从函数的角度看,就是寻求使一次函数值大于(或小于)反比例函数值的自变量x的取值范围;从函数图象的角度看,就是确定直线在双曲线上方(或下方)部分所有的点的横坐标所构成的集合.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| 捐款(元) | 5 | 10 | 50 | 100 |
| 人数 | 1 | 4 | 3 | 2 |
| A. | 100,50 | B. | 30,10 | C. | 10,10 | D. | 10,50 |
| 种树、种草每亩每年补粮补钱情况表 | ||
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
(2)若今年该农户增加40亩山坡地种树种草,要想年终政府补钱不少于12000元,至少需要增加安排多少亩山坡地种树?
| A. | ∠A=∠D,∠B=∠E,AB=DE | B. | ∠A=∠D,∠B=∠E,AC=DF | ||
| C. | AB=DE,∠B=∠E,BC=EF | D. | AB=DE,∠B=∠E,AC=DF |
 等边三角形ABC和等腰三角形ABD按如图所示的位置摆放,∠DAB=90°,AC与BD相交于点E,F为AD上一点,连接EF,CF,CF与BD交于点P,过点D作DG⊥AC于点G,过点B作BH⊥AC于点H.已知∠ECF=45°.
等边三角形ABC和等腰三角形ABD按如图所示的位置摆放,∠DAB=90°,AC与BD相交于点E,F为AD上一点,连接EF,CF,CF与BD交于点P,过点D作DG⊥AC于点G,过点B作BH⊥AC于点H.已知∠ECF=45°.