题目内容
11.(1)计算:$\frac{1}{\sqrt{5+2\sqrt{6}}}$+$\frac{1}{\sqrt{7+4\sqrt{3}}}$=2-$\sqrt{2}$(2)方程$\sqrt{2}$(x+1)=x+1的解是x=-1.
分析 (1)将分母中被开方数写成完全平方式,根据二次根式性质开方后分母有理化即可得;
(2)将x+1看做整体移项、合并后即可得x+1=0,从而得解.
解答 解:(1)原式=$\frac{1}{\sqrt{(\sqrt{2})^{2}+2×\sqrt{2}×\sqrt{3}+(\sqrt{3})^{2}}}$+$\frac{1}{\sqrt{{2}^{2}+2×2×\sqrt{3}+(\sqrt{3})^{2}}}$
=$\frac{1}{\sqrt{(\sqrt{2}+\sqrt{3})^{2}}}$+$\frac{1}{\sqrt{(2+\sqrt{3})^{2}}}$
=$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{2+\sqrt{3}}$
=$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$
=2-$\sqrt{2}$,
故答案为:2-$\sqrt{2}$;
(2)移项、合并,得:($\sqrt{2}-1$)(x+1)=0,
∴x+1=0,即x=-1,
故答案为:x=-1.
点评 本题主要考查二次根式的混合运算和解方程的能力,熟练掌握完全平方公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.点A与点B关于x轴对称,点B与点C关于原点对称,若点A的坐标是($\frac{x-a}{|x-a|}$,$\frac{2x-b}{\sqrt{4{x}^{2}-4bx+{b}^{2}}}$)($\frac{b}{2}$<x<a),则点C的坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
16.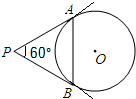 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
3.关于x的方程x2+(m-2)x+m+1=0有两个相等的实数根,则m的值是( )
| A. | 0 | B. | 8 | C. | 4$±\sqrt{2}$ | D. | 0或8 |
 如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,使点D正好落在AB边上,记落点为F,求sin∠AFE的值.
如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,使点D正好落在AB边上,记落点为F,求sin∠AFE的值. 如图,已知AB与CD交于点O,且△AOC≌△BOD,求证:AC∥BD.
如图,已知AB与CD交于点O,且△AOC≌△BOD,求证:AC∥BD.