某农场拟建两间矩形饲养室.一面靠现有墙.中间用一道墙隔开.并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体总长为27m.则能建成的饲养室面积最大为75m2．题目和参考答案——青夏教育精英家教网—

题目内容

20．

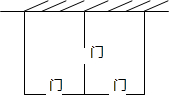某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为75m²．

分析设垂直于墙的材料长为x米，则平行于墙的材料长为27+3-3x=30-3x，表示出总面积S=x（30-3x）=-3x²+30x=-3（x-5）²+75即可求得面积的最值．

解答解：设垂直于墙的材料长为x米，
则平行于墙的材料长为27+3-3x=30-3x，
则总面积S=x（30-3x）=-3x²+30x=-3（x-5）²+75，
故饲养室的最大面积为75平方米，
故答案为：75．

点评本题考查了二次函数的应用，解题的关键是从实际问题中抽象出函数模型，难度不大．

练习册系列答案

相关题目

10．下列各组数据中，能构成三角形的是（　　）

11．

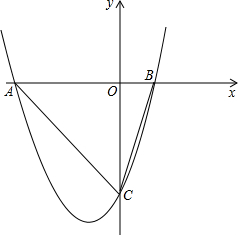已知抛物线y=x²+2x-3与x轴交于A，B（点A在点B的左侧）两单，与y轴交于点C．
（1）填空：点B的坐标是（1，0），直线AC的函数关系式为y=-x-3；
（2）设点D（-2，a），请问，当a为何值时，DB+DC值最小？
（3）若直线AC上是否存在一点P，使以点A、O、P为顶点的三角形与△ABC相似？若存在，请求出P点的坐标；若不存在，请说明理由．

8．

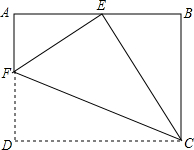如图，将一张矩形纸片ABCD沿CF折叠，使点D与AB的中点E重合，求$\frac{AF}{FD}$．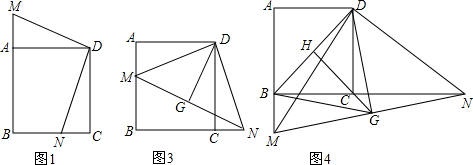

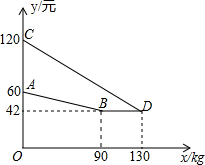15．已知四边形ABCD是正方形
（1）如图1．点M在边BA的延长线上，点N在边BC上，且AM=CN，连接MN，DM，DN，判断△DMN的形状（直接写出答案）．
（2）如图2，当店N在边AB上，点N在边BC的延长线上，AM=CN，连接MN，取线段MN的中点G，连接DG，DM，判断线段DG和线段MG的关系并说明理由．
（3）如图3，当点M在边AB的延长线上，点N在边BC的延长线上，AM=CN，连接MN，DM，DN，点G是线段MN的中点，连接BG，DG，连接GC并延长交BD于点H，若∠AMN=75°，判断线段GH和线段BD的关系并说明理由．

5．

某企业生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD、线段CD分别表示该产品每千克生产成本y₁（单位：元）、销售价y₂（单位：元）与产量x（单位：kg）之间的函数关系．
（1）请解释图中点D的横坐标、纵坐标的实际意义；
（2）求线段AB所表示的y₁与x之间的函数表达式；
（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？

12．

如图，PA和PB是⊙O的切线，点A和点B是切点，AC是⊙O的直径，已知∠P=40°，则∠ACB的大小是（　　）

9．计算：π⁰+2^-1-$\sqrt{\frac{1}{4}}$-|-$\frac{1}{3}$|

10．

如图A，B，C是⊙O上的三个点，若∠AOC=100°，则∠ABC等于（　　）

试题分类