题目内容
10.解下列不等式(组),并把它们的解集在数轴上表示出来:(1)$\frac{x-1}{2}$+1≥x
(2)1-$\frac{3x-5}{2}$≥$\frac{1}{3}$-$\frac{2x+1}{6}$
(3)$\left\{\begin{array}{l}{x-3(x-2)≤4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$
(4)$\left\{\begin{array}{l}{1-x>0}\\{2(x+5)>4}\end{array}\right.$.
分析 (1)根据解一元一次不等式基本步骤:去分母、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
(3)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集;
(4)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)去分母,得:x-1+2≥2x,
移项,得:x-2x≥1-2,
合并同类项,得:-x≥-1,
系数化为1,得:x≤1, ;
;
(2)去分母,得:6-3(3x-5)≥2-(2x+1),
去括号,得:6-9x+15≥2-2x-1,
移项,得:-9x+2x≥2-1-6-15,
合并同类项,得:-7x≥-20,
系数化为1,得:x≤$\frac{20}{7}$, ;
;
(3)解不等式x-3(x-2)≤4,得:x≥1,
解不等式$\frac{1+2x}{3}$>x-1,得:x≤4,
∴不等式组的解集为1≤x≤4, ;
;
(4)解不等式1-x>0,得:x<1,
解不等式2(x+5)>4,得:x>-3,
∴不等式组的解集为-3<x<1, .
.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知两个相似三角形的面积之比是4:9,那么这两个三角形周长的比是( )
| A. | 4:9 | B. | 9:4 | C. | 16:81 | D. | 2:3 |
18.下列二次根式中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{48}$ | C. | $\sqrt{6}$ | D. | $\sqrt{32}$ |
2. 一个空心的圆柱如图,那么它的左视图是( )
一个空心的圆柱如图,那么它的左视图是( )
 一个空心的圆柱如图,那么它的左视图是( )
一个空心的圆柱如图,那么它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
20.下列图形既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
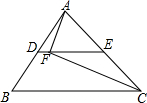 如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为14.
如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为14.