题目内容
13.反比例函数①y=$\frac{2}{x}$、②y=$\frac{1}{3x}$、③7y=-$\frac{10}{x}$、④y=$\frac{3}{100x}$的图象中.(1)在第一、三象限的是①②④,在第二、四象限的是③
(2)在其所在各个象限内,y随x的增大而增大的是③.
分析 (1)根据反比例函数的性质可知,当k>0时,函数图象在第一、三象限,当k<0时,函数图象在第二、四象限,从而可以解答本题;
(2)根据反比例函数的性质可知,当k<0时,y随x的增大而增大,从而可以解答本题.
解答 解:(1)∵在①y=$\frac{2}{x}$、②y=$\frac{1}{3x}$、④y=$\frac{3}{100x}$的k都>0,
∴在第一、三象限的是①②④,
∵③7y=-$\frac{10}{x}$中,k=$-\frac{10}{7}$<0,
∴在第二、四象限的是③,
故答案是:①②④,③;
(2)∵③7y=-$\frac{10}{x}$中,k=$-\frac{10}{7}$<0,
∴该函数的图象在第二、四象限,并且在每个象限内y随x的增大而增大,
故答案为③.
点评 本题考查反比例函数的性质,解题的关键是明确反比例函数的性质,会用性质解答问题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
3.关于反比例函数y=$\frac{3}{x}$的图象,下列说法正确的是( )
| A. | 两个分支关于原点成中心对称 | B. | 两个分支分布在第二、四象限 | ||
| C. | 两个分支关于x轴成轴对称 | D. | 必经过点(1,1) |
1.下列计算正确的是( )
| A. | 3a-2a=1 | B. | |-5|=5 | C. | $\sqrt{4}$=±2 | D. | 2-3=-6 |
18.-(-2)的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
 在平面直角坐标系xOy中,抛物线y=ax2-2x的对称轴为x=-1.
在平面直角坐标系xOy中,抛物线y=ax2-2x的对称轴为x=-1. 在直角△ABC中,∠ACB=90°,点E在AC边上,连结BE,作∠ACF=∠CBE交AB于点F,同时点D在BE上,且CD⊥AB.
在直角△ABC中,∠ACB=90°,点E在AC边上,连结BE,作∠ACF=∠CBE交AB于点F,同时点D在BE上,且CD⊥AB.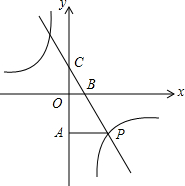 如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.
如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.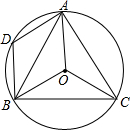 如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.
如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.