题目内容
4.己知:直线y=$\frac{a-1}{a}$x+$\frac{1}{a}$不过第二象限,求a的范围.分析 由一次函数不过第二象限可知,k>0且b<0,由此得出关于a的一元一次不等式组,解不等式组即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{\frac{a-1}{a}>0}\\{\frac{1}{a}<0}\end{array}\right.$,
解得:a<0.
点评 本题考查了一次函数图象与系数的关系,解题的关键是由函数图象在一、三、四象限得出关于a的不等式组.本题属于基础题,难度不大,解决该题型题目时,根据函数图形所在的象限得出k、b的取值范围是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.抛物线y=2x2+4x+3的图象与x轴有( )
| A. | 一个交点 | B. | 两个交点 | C. | 没有交点 | D. | 无法确定 |
12.下列计算正确的是( )
| A. | $\sqrt{20}=2\sqrt{10}$ | B. | $\sqrt{4}-\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
19.下列计算正确的是( )
| A. | 2x2•4x2=8x2 | B. | x5÷x-1=x4 | C. | (x4)4=x16 | D. | (-3x2)3=-9x6 |
9.下列计算正确的是( )
| A. | a2•a4=a6 | B. | -(a-b)=-a-b | C. | (a3b)2=a6b | D. | 3a2-a2=2 |
14.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | a2•a3=a6 | C. | (a+1)2=a2+1 | D. | (-a2)2=a4 |
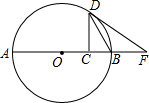 如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.
如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.