题目内容
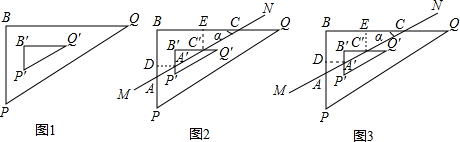
1.如图①是一个含有30°角的直角三角板的图片,其内外两个三角形△P′B′Q′与△PBQ的三边分别平行,如图②,现在任意画一条直线MN与这两个三角形的四条直角边分别交于点A、A′、C、C′,锐角∠BCA等于α,C′E等于B′Q′与BQ之间的距离,A′D等于B′P′与BP之间的距离.(1)求证:△DA′A∽△ECC′;
(2)在图②中,如果A′D=C′E,求$\frac{AA′}{CC′}$等于多少.(结果用含α的三角函数的式子表示)此时AA′与CC′可能相等吗?若能相等,求出相应的α值;若不能相等,说明理由;
(3)如图③如果保持图片中的△PBQ不动,将△P′B′Q′适当上下平移,使A′D=nC′E,则$\frac{AA′}{CC′}$等于$\frac{nsinα}{cosα}$.(用含α的三角函数的式子表示)
分析 (1)求出两个角分别相等,根据相似三角形的判定定理推出即可;
(2)解直角三角形求出AA′、CC′的值,再代入求出即可;
(3)解直角三角形求出AA′、CC′的值,再代入求出即可.
解答 (1)证明:∵C′E等于B′Q′与BQ之间的距离,A′D等于B′P′与BP之间的距离,
∴AB∥C′E,∠ADA′=∠C′EC=90°,
∴∠DAA′=∠EC′C,
∴∠DA′A=∠ECC′=α,
∴△DA′A∽△ECC′;
(2)解:在Rt△ADA′和Rt△C′EC中,
AA′=$\frac{A′D}{cosα}$,CC′=$\frac{C′E}{sinα}$,
∵A′D=C′E,
∴$\frac{AA′}{CC′}$=$\frac{sinα}{cosα}$,
AA′与CC′能相等,
当相等时,sinα=cosα,
即α=45°;
(3)在Rt△ADA′和Rt△C′EC中,
AA′=$\frac{A′D}{cosα}$,CC′=$\frac{C′E}{sinα}$,
∵A′D=nC′E,
∴$\frac{AA′}{CC′}$=$\frac{nsinα}{cosα}$,
故答案为:$\frac{nsinα}{cosα}$.
点评 本题考查了几何变换,相似三角形的判定,解直角三角形的应用,能通过解直角三角形求出AA′和CC′的长是解此题的关键,求解过程类似.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
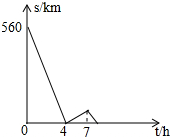 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
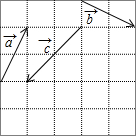 如图,由单位小正方形拼成的5×5的大正方形中.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$.求作:
如图,由单位小正方形拼成的5×5的大正方形中.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$.求作: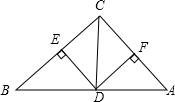 如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,若CE=2,求四边形CEDF的面积.
如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,若CE=2,求四边形CEDF的面积.