题目内容
11.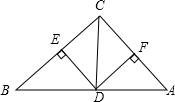 如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,若CE=2,求四边形CEDF的面积.
如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,若CE=2,求四边形CEDF的面积.
分析 根据垂直和角平分线性质得出DE=DF,∠ECF=∠CED=∠CFD=90°,根据正方形的判定推出四边形CEDF是正方形,求出EC=DE=DF=CF=2即可.
解答 解:∵∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∠ECF=∠CED=∠CFD=90°,
∴四边形CEDF是正方形,
∴EC=DE=DF=CF=2,
∴四边形CEDF的面积是2×2=4.
点评 本题考查了角平分线性质,正方形的性质和判定的应用,解此题的关键是推出四边形CEDF是正方形,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
16.下列各组数是勾股数的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 3.6,4,8.6 | D. | 9,40,41 |
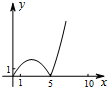
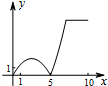
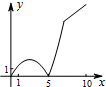
 如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )
如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )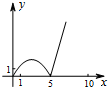
 如图,△ABC中,DE是BC的垂直平分线.若AC=8cm,△ABE的周长为14cm,则AB的长为6cm.
如图,△ABC中,DE是BC的垂直平分线.若AC=8cm,△ABE的周长为14cm,则AB的长为6cm.