题目内容
已知抛物线y=-x2+6x+m上有三点：A（1，y1）、B（2，y2）、C（3+
，y3），则y1、y2、y3的大小关系是（ ）
| 2 |
| A、y2＜y1＜y3 |
| B、y1＜y2＜y3 |
| C、y1＜y3＜y2 |
| D、y3＜y1＜y2 |
考点：二次函数图象上点的坐标特征
专题：计算题
分析：先确定抛物线的开口向下，对称轴为直线x=-3，根据二次函数的性质得到抛物线上的点离对称轴越近，对应的函数值越大，然后通过比较点A、B、C到直线x=3的距离来比较y1、y2、y3的大小关系．
解答：解：抛物线y=-x2+6x+m的开口向下，对称轴为直线x=-
=3，
∵A点（1，y1）到直线x=3的距离为2、B点（2，y2）到直线x=3的距离为1，、C点（3+
，y3）到直线x=3的距离为
，
∴y1＜y3＜y2．
故选C．
| 6 |
| 2×(-1) |
∵A点（1，y1）到直线x=3的距离为2、B点（2，y2）到直线x=3的距离为1，、C点（3+
| 2 |
| 2 |
∴y1＜y3＜y2．
故选C．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．
练习册系列答案
相关题目
如图，AB是⊙O的直径，点C、D都在⊙O上，若∠C=20°，则∠ABD的度数等于计算-（-2014）的结果是（ ）
| A、-2014 | ||
| B、2014 | ||
C、-
| ||
D、
|
已知一次函数y=kx+b中，k＜0，b＜0，请问这函数不经过什么象限？（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知点A（2，y1）和点B（m，y2）是抛物线y=x2-2x上两点，且y2＞y1，则m的取值范围是（ ）
| A、m＞2 |
| B、m≤0或m≥2 |
| C、0＜m＜2 |
| D、m＜0或m＞2 |
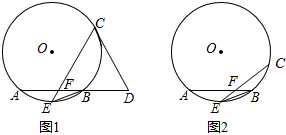如图1，在⊙O中，E是
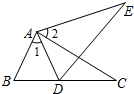如图，在△ABC和△ADE中，B、D、C三点在同一直线上．有以下四个条件：